
分析 设点D是AF2的中点,由$\overrightarrow{M{F}_{1}}$+2$\overrightarrow{M{F}_{2}}$+2$\overrightarrow{MA}$=0⇒若$\overrightarrow{M{F}_{1}}$=-2($\overrightarrow{M{F}_{2}}$+$\overrightarrow{MA}$)=-4$\overrightarrow{MD}$,
即三点F1、M、D三点共线,且点M是靠近D的5等分点,△AF1F2与△AMF2的面积比为5:1;
如图$\overrightarrow{M{F}_{1}}+2\overrightarrow{M{F}_{2}}=\overrightarrow{MF}$,有$\frac{M{F}_{2}}{{F}_{1}F}=\frac{MH}{HF}=1:2$,由$\overrightarrow{M{F}_{1}}$+2$\overrightarrow{M{F}_{2}}$+2$\overrightarrow{MA}$=0,得2$\overrightarrow{AM}=\overrightarrow{MF}$,⇒AM:MH=3:2,⇒△AF1F2与△AMF1F2的面积比为5:2
解答 解:设点D是AF2的中点,
∵$\overrightarrow{M{F}_{1}}$+2$\overrightarrow{M{F}_{2}}$+2$\overrightarrow{MA}$=0⇒若$\overrightarrow{M{F}_{1}}$=-2($\overrightarrow{M{F}_{2}}$+$\overrightarrow{MA}$)=-4$\overrightarrow{MD}$,
∴三点F1、M、D三点共线,且点M是靠近D的5等分点,
△AF1F2与△AMF2的面积比为5:1;
如图$\overrightarrow{M{F}_{1}}+2\overrightarrow{M{F}_{2}}=\overrightarrow{MF}$,有$\frac{M{F}_{2}}{{F}_{1}F}=\frac{MH}{HF}=1:2$,
由$\overrightarrow{M{F}_{1}}$+2$\overrightarrow{M{F}_{2}}$+2$\overrightarrow{MA}$=0,得2$\overrightarrow{AM}=\overrightarrow{MF}$,⇒AM:MH=3:2,
∴△AF1F2与△AMF1F2的面积比为5:2
又∵△AMF2与△AMF1F2的面积比为AF2:F1F2=1:2,
AF2:F1F2:AF1=1:2:2,∴2a=3c,
椭圆的离心率为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$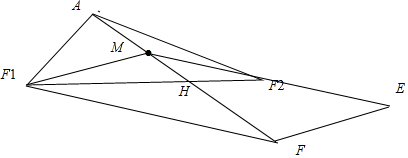
点评 本题考查了椭圆的离心率、向量的线性运算,属于难题.


科目:高中数学 来源: 题型:解答题
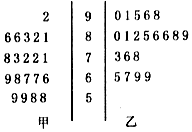 某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:
某大学高等数学老师这学期分别用A、B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图如图:| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | [3,+∞) | C. | (0,3) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可由函数g(x)=cos2x的图象向左平移$\frac{π}{3}$个单位而得 | |
| B. | 可由函数g(x)=cos2x的图象向右平移$\frac{π}{3}$个单位而得 | |
| C. | 可由函数g(x)=cos2x的图象向左平移$\frac{π}{6}$个单位而得 | |
| D. | 可由函数g(x)=cos2x的图象向右平移$\frac{π}{6}$个单位而得 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{π}{2},-\frac{π}{4})$ | B. | $(-\frac{π}{4},\frac{π}{2})$ | C. | $(\frac{π}{2},π)$ | D. | $(\frac{3π}{2},2π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com