考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
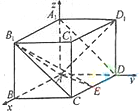
分析:(1)由题意及所给的图形,分别以AB,AD,AA
1为x轴、y轴、z轴建立空间直角坐标系,设AB=a,给出图形中各点的坐标,可求出向量
、
的坐标,验证其数量积为0即可得出结论;
(2)由题设条件,可求夹二面角的两个平面的法向量,可得两平面的夹角的余弦,即可求二面角
A-B1E-1的大小;
(3)由题意,可先假设在棱AA
1上存在一点P(0,0,z
0),使得DP∥平面B
1AE,求出平面B
1AE法向量,利用法向量与直线DP的方向向量数量积为0,由此方程解出z
0的值,若能解出,则说明存在,若不存在符合条件的t的值,说明不存在这样的点P满足题意.
解答:
解:(1)分别以AB,AD,AA
1为x轴、y轴、z轴建立空间直角坐标系,设AB=a则A(0,0,0),D(0,1,0),D
1(0,1,1),E(
,1,0),B
1(a,0,1),
∴
=(0,1,1),
=(-
,1,-1),
=(a,0,1),
=(
,1,0),
∵
•
=1-1=0
∴B
1E⊥AD
1,
∴直线B
1E与直线AD
1所成的角的余弦值为0;
(2)连接A
1D,B
1C,由长方体ABCD-A
1B
1C
1D
1及AA
1=AD=1,得AD
1⊥A
1D.
∵B
1C∥A
1D,∴AD
1⊥B
1C.
由(1)知,B
1E⊥AD
1,且B
1C∩B
1E=B
1.
∴AD
1⊥平面DCB
1A
1,
∴
是平面A
1B
1E的一个法向量,此时
=(0,1,1)
AB=2,设平面B
1AE的法向量
=(x,y,z),则
=(2,0,1),
=(1,1,0)
∵
⊥平面B
1AE,∴
⊥,⊥,
得
取x=1,使得平面B
1AE的一个法向量
=(1,-1,2),
设
与
所成的角为θ,则
cosθ=
=-
∴二面角A-B
1E-A
1的大小为30°;
(3)假设在棱AA
1上存在一点P(0,0,z
0)使得DP∥平面B
1AE.此时
=(0,-1,z0)又设AB的长度为a,平面B
1AE的法向量
=(x,y,z),则
=(a,0,1),=(,1,0)∵
⊥平面B
1AE∴
⊥,⊥得
取x=1,使得平面B
1AE的一个法向量
=(1,,-a)要使DP∥平面B
1AE,只要
⊥,有
-az0=0,解得
z0=又DP?平面B
1AE,∴存在点P,满足DP∥平面B
1AE,此时
AP=.
点评:本题考查利用空间向量这一工具求二面角,证明线面平行,解题的关键是建立恰当的坐标系及空间位置关系与向量的对应.

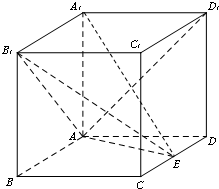 在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.
在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
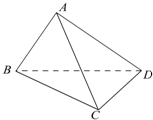 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.