解答:
解:由题意可知:切线PA、PB的斜率都存在,分别为k
1,k
2,切点A(x
1,y
1),B(x
2,y
2).
设过点P的抛物线的切线l:y=k(x-m)+n,代入x
2=4y,
可得x
2-4kx+(4km-4n)=0(*).
∵直线l与抛物线相切,∴△=16k
2-4×(4km-4n)=0,化为k
2-km+n=0.
∴k
1+k
2=m,k
1k
2=n.(**)
此时,x
1=2k
1,y
1=
=
k12;同理,x
2=2k
2,y
2=
k22.
∴
•=(x
1-m)(x
2-m)+(y
1-n)(y
2-n)
=(2k1-m)(2k2-m)+(k12-n)(k22-n)
=4k
1k
2-2m(k
1+k
2)+m2+(k1k2)2-n[(k1+k2)2-2k1k2]+n2
=4n-2m
2+m
2+n
2-n(m
2-2n)+n
2=4n
2+4n-m
2(1+n).
∵点P(m,n)在圆C
1上,
∴m
2+(n+1)
2=
,即 m
2=
-(n+1)
2,
代入上式可得
•=n
3+7n
2+
n+
,
考查函数f(n)═n
3+7n
2+
n+
(-1-
≤n≤-1+
),.
求得f′(n)=3n
2+14n+
=
(2n+1)6n+25),
令f′(n)=0,解得n=-
,或 n=-
.
当n∈(-1-
-
)时,f′(n)<0,f(n)为减函数,
当n∈(-
,-1+
)时,f′(n)>0,f(n)为增函数,
故当n=-
f(n)取得最小值为f(-
)=-
,
此时对应的点P(±
,-
).



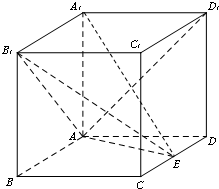 在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.
在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.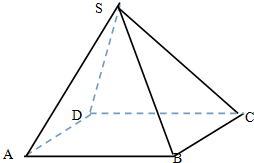 如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.
如图四棱锥S-ABCD中,底面是边长为2厘米的正方形,侧棱长都是2厘米.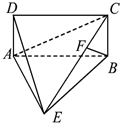 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.