
分析 (1)根据三角函数的性质的关于x的不等式组,解出即可;
(2)将f(x)=2+log3x(0<x≤9)代入y=[f(x)]2+f(x2)中,整理化简为关于log3x的函数,利用换元法求最值.
解答 解:(1)∵x∈(0,9],
∴$\left\{\begin{array}{l}{0<2sinx-1≤9}\\{0<3\sqrt{3}tanx≤9}\end{array}\right.$,解得:2kπ+$\frac{π}{6}$<x≤2kπ+$\frac{π}{3}$,
∴函数g(x)的定义域是:(2kπ+$\frac{π}{6}$,2kπ+$\frac{π}{3}$];
(2)y=[f(x)]2+f(x2)=(log3x)2+6log3x+6,
∵f(x)=2+log3x(0<x≤9),
∴$\left\{\begin{array}{l}{0<x≤9}\\{{0<x}^{2}≤9}\end{array}\right.$,解得;0<x≤3,
∴y=[f(x)]2+f(x2)=(log3x)2+6log3x+6的定义域是{x|0<x≤3}.
令log3x=t,因为0<x≤3,所以t≤1,
则上式变为y=t2+6t+6,t≤1,
y=t2+6t+6在(∞,-3)递减,在(-3,1]上是增函数,
当t=-3时,y取最小值-3.
点评 本题考查了对数函数以及三角函数的性质,考查换元法求函数的值域问题,在使用换元法时,注意范围.


科目:高中数学 来源: 题型:选择题
| A. | ${A}_{5}^{2}$${A}_{2}^{2}$ | B. | ${A}_{7}^{7}$-${A}_{2}^{2}$${A}_{6}^{6}$ | ||
| C. | ${A}_{7}^{7}$-${A}_{6}^{6}$ | D. | ${C}_{10}^{8}$0.820.28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
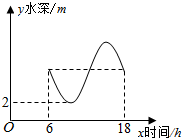 如图,某港口一天6时到18时的水深变化曲线近似满足函数y=sin($\frac{π}{6}$x+φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为4.
如图,某港口一天6时到18时的水深变化曲线近似满足函数y=sin($\frac{π}{6}$x+φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
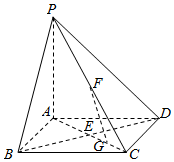 如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 30 | D. | 42 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com