
分析 (1)由正弦定理直接求解B的大小.
(2)利用三角形内角和定理,消去C,利用和与差公式打开,化简可得A与B的关系,即可求解.
解答 解:(1)c=2,C=$\frac{π}{3}$.b=$\frac{{2\sqrt{6}}}{3}$,
由正弦定理:得$\frac{2}{sin\frac{π}{3}}=\frac{\frac{2\sqrt{6}}{3}}{sinB}$,
可得sinB=$\frac{\sqrt{2}}{2}$,
∵0<B<120°,
∴B=45°.
(2)由sinC=sin(A+B),
∴sinC+sin(B-A)=2sin2A,即sin(A+B)+sin(B-A)=2sin2A,
可得:2sinBcosA=4sinAcosA,即cosA(sinB-2sinA)=0,
∴cosA=0或sinB=2sinA,
当cosA=0时,
A=$\frac{π}{2}$,
∵C=$\frac{π}{3}$.
∴B=$\frac{π}{6}$,
△ABC的面积S=$\frac{2\sqrt{3}}{3}$;
当sinB=2sinA,即b=2a时,
由余弦定理:c2=a2+b2-2abcosC.
可得:ab=$\frac{8}{3}$,
△ABC的面积S=$\frac{1}{2}$absinC=$\frac{2\sqrt{3}}{3}$;
点评 本题考查了正余弦定理,三角形内角和定理,以及和与差公式的运用和计算能力.属于基础题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
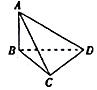 要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )
要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )| A. | 40m | B. | 20m | C. | 305m | D. | (20$\sqrt{6}$-40)m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | (0,e) | C. | [1,e) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|0≤x<2} | C. | {x|x<2} | D. | {x|x≥2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com