
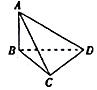
 要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )
要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )| A. | 40m | B. | 20m | C. | 305m | D. | (20$\sqrt{6}$-40)m |
分析 设出AB=x,由题意将BD、DC用x来表示,然后在△DBC中利用余弦定理建立方程求得x,即可得到电视塔的高度.
解答 解:由题题意,设AB=x,则BD=$\sqrt{3}$x,BC=x
在△DBC中,∠BCD=120°,CD=40,
∴根据余弦定理,得BD2=BC2+CD2-2BC•CD•cos∠DCB
即:($\sqrt{3}$x)2=(40)2+x2-2×40•x•cos120°
整理得x2-20x-800=0,解之得x=40或x=-20(舍去)
即所求电视塔的高度为40米.
故选:A.
点评 本题给出实际应用问题,求电视塔的高度.着重考查了解三角形的实际应用的知识,考查了运用数学知识、建立数学模型解决实际问题的能力.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,2x<0 | B. | ?x∈R,2x<0 | C. | ?x∈R,2x≤0 | D. | ?x∈R,2x≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a1+a2>0,则a2+a3>0 | B. | 若a1+a2<0,则a2+a3<0 | ||
| C. | 若0<a1<a2,则a2>$\sqrt{{a}_{1}{a}_{3}}$ | D. | 若a1<0,则(a2-a1)(a2-a3)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com