
分析 (I)利用和与差的公式,构造思想,可得sinβ的值.
(II)根据二倍角公式和同角函数关系式,即可求解.
解答 解(I)∵$0<β<\frac{π}{2}$,$0<α<\frac{π}{2}$,
0<α+β<π,
cosα=$\frac{3}{5}$,
∴sinα=$\frac{4}{5}$,
sin(α+β)=$\frac{12}{13}$,
那么:sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=$\frac{16}{65}$;
(II)由(I)sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$,
那么sin2α=2sinαcosα=$\frac{24}{25}$,
cos2α=$\frac{9}{25}$,
cos2α=1-2sin2α=$-\frac{7}{25}$,
∴$\frac{sin2α}{{{{cos}^2}α+cos2α}}$=$\frac{\frac{24}{25}}{\frac{9}{25}-\frac{7}{25}}=12$.
点评 本题考查了和与差的公式,二倍角公式和同角函数关系式的计算.属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | x1+x2>0 | B. | x1+x2<0 | C. | x1+x2=0 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 周期是$\frac{π}{2}$ | ||
| C. | 关于直线$x=\frac{π}{12}$对称 | D. | 关于点$({-\frac{π}{4},0})$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥$\frac{5}{2}$ | B. | m>$\frac{5}{2}$ | C. | m≤$\frac{5}{2}$ | D. | m<$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
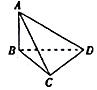 要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )
要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )| A. | 40m | B. | 20m | C. | 305m | D. | (20$\sqrt{6}$-40)m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | (0,e) | C. | [1,e) | D. | (0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com