
分析 把①②代入exf(x),变形为指数函数判断;把③④代入exf(x),求导数判断.
解答 解:对于①,f(x)=2-x,则g(x)=exf(x)=${e}^{x}•{2}^{-x}=(\frac{e}{2})^{x}$为实数集上的增函数;
对于②,f(x)=3-x,则g(x)=exf(x)=${e}^{x}•{3}^{-x}=(\frac{e}{3})^{x}$为实数集上的减函数;
对于③,f(x)=x3,则g(x)=exf(x)=ex•x3,
g′(x)=ex•x3+3ex•x2=ex(x3+3x2)=ex•x2(x+3),当x<-3时,g′(x)<0,
∴g(x)=exf(x)在定义域R上先减后增;
对于④,f(x)=x2+2,则g(x)=exf(x)=ex(x2+2),
g′(x)=ex(x2+2)+2xex=ex(x2+2x+2)>0在实数集R上恒成立,
∴g(x)=exf(x)在定义域R上是增函数.
∴具有M性质的函数的序号为①④.
故答案为:①④.
点评 本题考查函数单调性的性质,训练了利用导数研究函数的单调性,是中档题.


科目:高中数学 来源: 题型:选择题
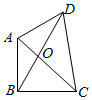 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )| A. | I1<I2<I3 | B. | I1<I3<I2 | C. | I3<I1<I2 | D. | I2<I1<I3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,2] | C. | (-2,1) | D. | [-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{18}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -1或$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | -1或$-\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com