
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,三角形
,三角形![]() 的两条边
的两条边![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(I)求点![]() 的轨迹方程;
的轨迹方程;
(II)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 面积
面积![]() 关于
关于![]() 的表达式.
的表达式.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)设点![]() 的坐标为
的坐标为![]() ,由点
,由点![]()
![]() ,
,![]() 求得
求得![]() ,利用斜率之积是
,利用斜率之积是![]() ,化简可得结果;(Ⅱ)直线
,化简可得结果;(Ⅱ)直线![]() 的方程为
的方程为![]() ,求得点
,求得点![]() ,则
,则![]() ,将
,将![]() 与
与![]() 联立,得
联立,得![]() ,求得
,求得![]() 的坐标,可得直线
的坐标,可得直线![]() 的方程,求得点
的方程,求得点![]() 坐标,由两点间距离公式与三角形面积公式可得结果.
坐标,由两点间距离公式与三角形面积公式可得结果.
(Ⅰ)设点M的坐标为(x,y),因为点A的坐标是(-2,0),
所以,直线AM的斜率![]()
同理,直线BM的斜率![]()
由已知又![]()
化简,得点M的轨迹方程![]()
(Ⅱ)直线AM的方程为x=my-2(m≠0),与直线l的方程x=2联立,可得点![]() ,故
,故![]() .
.
将x=my-2与![]() 联立,消去x,整理得
联立,消去x,整理得![]() ,解得y=0,或
,解得y=0,或![]() .
.
由题设,可得点![]() .由
.由![]() ,
,
可得直线MQ的方程为![]() ,
,
令y=0,解得![]() ,故
,故![]() .
.
所以![]() .
.
所以△APD的面积:
![]()


科目:高中数学 来源: 题型:
【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.

(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 表示k个数字均为1的十进制数(如
表示k个数字均为1的十进制数(如![]() =1,
=1,![]() =111),定义
=111),定义![]() 。
。
(1)对于任意正整数m、n,令![]() ,写出一个关于f(m,n)的递推关系式,并证明之;
,写出一个关于f(m,n)的递推关系式,并证明之;
(2)证明:对于任意正整数m、n,{m+n}!均可以被{m}!.{n}!整除。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在![]() 内现将这100名学生的成绩按照
内现将这100名学生的成绩按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组后,得到的频率分布直方图如图所示,则下列说法正确的是
分组后,得到的频率分布直方图如图所示,则下列说法正确的是![]()
![]()

A. 频率分布直方图中a的值为![]()
B. 样本数据低于130分的频率为![]()
C. 总体的中位数![]() 保留1位小数
保留1位小数![]() 估计为
估计为![]() 分
分
D. 总体分布在![]() 的频数一定与总体分布在
的频数一定与总体分布在![]() 的频数相等
的频数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从广安市某中学校的![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于![]() cm和
cm和![]() cm之间,将测量结果按如下方式分成八组:第一组
cm之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,...,第八组
,...,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为![]() 人.
人.
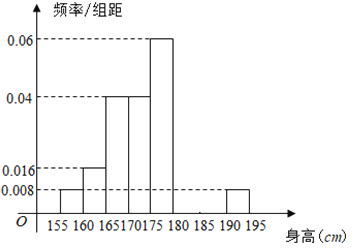
(1)求第七组的频率;
(2)估计该校![]() 名男生的身高的中位数。
名男生的身高的中位数。
(3)若从样本中身高属于第六组和第八组的所有男生中随机抽取两名男生,求抽出的两名男生是同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .三角形
.三角形![]() 的两条边
的两条边![]() ,
,![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com