
分析 把已知等式两边展开两角和与差的正切,整理后化切为弦,进一步整理得答案.
解答 证明:由3tan(α-$\frac{π}{12}$)=tan(α+$\frac{π}{12}$),得
$3\frac{tanα-tan\frac{π}{12}}{1+tanαtan\frac{π}{12}}=\frac{tanα+tan\frac{π}{12}}{1-tanαtan\frac{π}{12}}$,
整理得:tanα($1+ta{n}^{2}\frac{π}{12}$)-2tan$\frac{π}{12}$(1+tan2α)=0,
即$tanα•\frac{1}{co{s}^{2}\frac{π}{12}}-2tan\frac{π}{12}•\frac{1}{co{s}^{2}α}=0$,
∴$\frac{sinα}{cosα}•\frac{2}{1+cos\frac{π}{6}}-2•\frac{1-cos\frac{π}{6}}{sin\frac{π}{6}}•\frac{1}{co{s}^{2}α}=0$,
则$\frac{sinα}{1+\frac{\sqrt{3}}{2}}-\frac{1-\frac{\sqrt{3}}{2}}{\frac{1}{2}cosα}=0$,
∴$\frac{\frac{1}{2}sinαcosα-(1-\frac{\sqrt{3}}{2})(1+\frac{\sqrt{3}}{2})}{\frac{1}{2}(1+\frac{\sqrt{3}}{2})cosα}=0$,
∴$\frac{1}{4}sin2α={1}^{2}-(\frac{\sqrt{3}}{2})^{2}=\frac{1}{4}$,
即sin2α=1.
点评 本题考查两角和与差的正切函数,考查了同角三角函数的基本关系式的应用,关键是熟练记忆有关公式,是中档题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:解答题
已知函数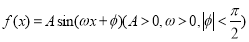 的部分图象如图所示.
的部分图象如图所示.
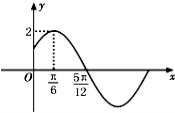
(1)求函数f(x)的解析式;
(2)当 ,
,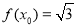 ,若g(x)=1+2cos2x,求g(x0)的值;
,若g(x)=1+2cos2x,求g(x0)的值;
(3)若h(x)=1+2cos2x+a,且方程f(x)﹣h(x)=0在 上有解,求实数a的取值范围.
上有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:填空题
某公司有工程师6人,技术员12人,技工18人,要从这些人中抽取n个人参加科技大会.如果采用系统抽样和分层抽样的方法抽取,不用剔除个体,如果参会人数增加1个,则在采用系统抽样时,需要在总体中先剔除1个个体,则n=_______.
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲
设函数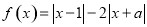 .
.
(1)当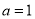 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式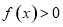 ,在
,在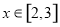 上恒成立,求
上恒成立,求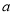 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
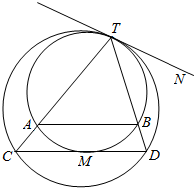 如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.
如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com