Question

17．我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市为了节约生活用水，计划在本市试行居民生活用水定额管理（即确定一个居民月均用水量标准0〜3.5，用水量不超过a的部分按照平价收费，超过a的部分按照议价收费）．为了较为合理地确定出这个标准，通过抽样获得了 100位居民某年的月均用水量（单位：t），制作了频率分布直方图．
（1）由于某种原因频率分布直方图部分数据丢失，请在图中将其补充完整；
（2）用样本估计总体，如果希望80%的居民每月的用水量不超出标准0〜3.5，则月均用水量的最低标准定为多少吨，请说明理由；
（3）从频率分布直方图中估计该100位居民月均用水量的平均数（同一组中的数据用该区间的中点值代表）．

Answer 1

分析 （1）根据频率和为1计算小组[1.5，2）的频率以及对应小矩形的高；
（2）月均用水量的最低标准应定为2.5吨，此时保证80%的居民每月的用水量不超出标准；
（3）根据频率分布直方图计算这100位居民月均用水量的平均数．

解答 解：（1）根据频率和为1，计算小组[1.5，2）的频率为
1-（0.10+0.20+0.30+0.60+0.30+0.10）×0.5=0.2，
对应小矩形的高为$\frac{0.2}{\frac{1}{2}}$=0.4，把频率分布直方图补充完整如下；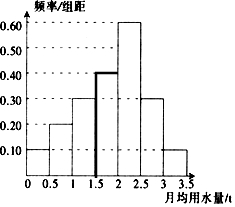

（2）月均用水量的最低标准应定为2.5吨，
样本中月均不低于2.5吨的居民有20位，占样本总体的20%，
由样本估计总体，要保证80%的居民每月的用水量不超出标准，
月均用水量的最低标准应定为2.5吨；
（3）估计频率分布直方图，计算这100位居民月均用水量的平均数为
0.5×（$\frac{1}{4}$×0.10+$\frac{3}{4}$×0.20+$\frac{5}{4}$×0.30+$\frac{7}{4}$×0.40+$\frac{9}{4}$×0.60+$\frac{11}{4}$×0.30+$\frac{13}{4}$×0.10）=1.875．

点评 本题考查了频率分布直方图的应用问题，是基础题．