Question

17．已知△ABC的外接圆的圆心为O，半径为1，若$\overrightarrow{AB}$+$\overrightarrow{AC}$=2$\overrightarrow{AO}$，且|$\overrightarrow{OA}$|=|$\overrightarrow{AC}$|，则向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$方向上的投影为$\frac{3}{2}$．

Answer 1

分析 根据已知条件便可知道O为BC边的中点，∠BAC=90°，△AOC为等边三角形，所以得到∠BOD=120°，∠ABO=30°，从而根据余弦定理求出$|\overrightarrow{BA}|=\sqrt{3}$，根据投影公式即可求得答案．

解答 解：如图，取BC边的中点D，连接AD，则：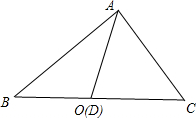
$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}=2\overrightarrow{AO}$；
∴O和D重合，O是△ABC外接圆圆心，$|\overrightarrow{OA}|=|\overrightarrow{AC}|$；
∴∠BAC=90°，∠BOA=120°，∠ABO=30°；
又|OA|=|OB|=1；
∴在△AOB中由余弦定理得：
$|\overrightarrow{AB}{|}^{2}=1+1-2•（-\frac{1}{2}）=3$，$|\overrightarrow{AB}|=\sqrt{3}$，∠ABO=30°；
∴向量$\overrightarrow{BA}$在向量$\overrightarrow{BC}$方向上的投影为$|\overrightarrow{BA}|•cos∠ABO=\frac{3}{2}$．
故答案为：$\frac{3}{2}$．

点评 考查三角形外心的概念，向量加法的平行四边形法则，直径对的圆周角为直角，以及余弦定理，一个向量在另一个向量方向上的投影公式．