
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成直二面角 ,如图二,在二面角
,如图二,在二面角 中.
中.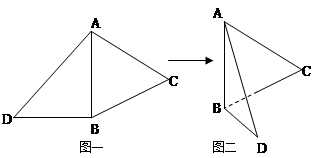
(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD成的角的正弦值。
(1)根据线面垂直的性质定理来得到线线垂直的证明。关键的一步是利用面ABD 面ABC,得到
面ABC,得到 BD
BD 面ABC,加以证明。
面ABC,加以证明。
(2) 2 (3)
(3)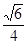
解析试题分析: 解:(1)依题意,面ABD 面ABC,AB是交线,
面ABC,AB是交线,
而BD AB,
AB, BD
BD 面ABC,又AC
面ABC,又AC 面ABC,
面ABC, BD⊥AC; 4分
BD⊥AC; 4分
(2)由(1)知,BD面ABC,而BC 面ABC,
面ABC, BD⊥BC;Rt
BD⊥BC;Rt DBC中,BC=BA=2,BD=2,
DBC中,BC=BA=2,BD=2, DC=
DC=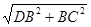 =
=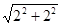 =2
=2 ; 8分
; 8分
(3)取AB的中点H,连CH、DH和DC,
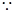 △ABC是正三角形,
△ABC是正三角形, CH
CH AB,又
AB,又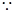 面ABC
面ABC 面ABD,
面ABD, CH
CH 面ABD,
面ABD, DH是DC在面ABD内的射影,
DH是DC在面ABD内的射影,
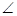 CDH是DC与面ABD成的角。
CDH是DC与面ABD成的角。
而CH=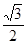 BC=
BC= ,由(2)DC=2
,由(2)DC=2 ,
, sin
sin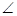 CDH=
CDH=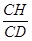 =
=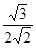 =
=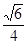 即为所求。 12分
即为所求。 12分
考点:空间中点线面的位置关系
点评:解决该试题的关键是熟练的运用判定定理和性质定理得到垂直的证明,以及角的求解,属于基础题。


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
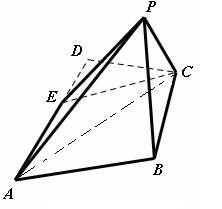
如图,在四边形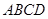 中,
中,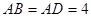 ,
,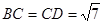 ,点
,点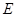 为线段
为线段 上的一点.现将
上的一点.现将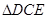 沿线段
沿线段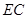 翻折到
翻折到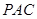 (点
(点 与点
与点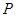 重合),使得平面
重合),使得平面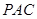
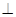 平面
平面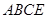 ,连接
,连接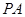 ,
,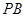 .
.
(Ⅰ)证明: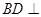 平面
平面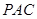 ;
;
(Ⅱ)若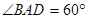 ,且点
,且点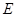 为线段
为线段 的中点,求二面角
的中点,求二面角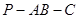 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知三棱锥S—ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心.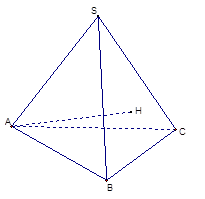
(1)求证:BC⊥SA
(2)若S在底面ABC内的射影为O,证明:O为底面△ABC的中心;
(3)若二面角H—AB—C的平面角等于30°,SA=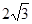 ,求三棱锥S—ABC的体积.
,求三棱锥S—ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.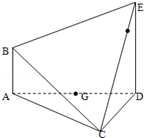
(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求平面BCE与平面ACD所成锐二面角的大小;
(3)求点G到平面BCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45o,F为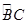 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).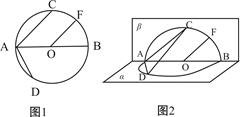
(Ⅰ)求证:OF//平面ACD;
(Ⅱ)在 上是否存在点
上是否存在点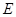 ,使得平面
,使得平面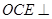 平面ACD?若存在,试指出点
平面ACD?若存在,试指出点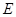 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=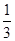 BB1,C1F=
BB1,C1F=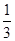 CC1.
CC1.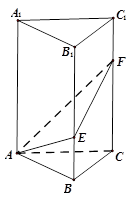
(1)求异面直线AE与A1 F所成角的大小;
(2)求平面AEF与平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知ABCD是矩形,AD=2AB,E,F分别是线段AB,BC的中点,PA⊥平面ABCD.
(Ⅰ)求证:DF⊥平面PAF;
(Ⅱ)在棱PA上找一点G,使EG∥平面PFD,当PA=AB=4时,求四面体E-GFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知四棱锥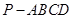 中
中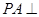 平面
平面 ,
,
且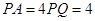 ,底面为直角梯形,
,底面为直角梯形,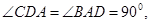
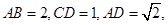
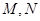 分别是
分别是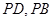 的中点.
的中点.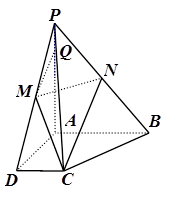
(1)求证: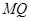 // 平面
// 平面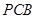 ;
;
(2)求截面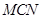 与底面
与底面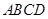 所成二面角的大小;
所成二面角的大小;
(3)求点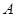 到平面
到平面 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com