Question

12．函数f（x）=$\sqrt{{x^2}-6x+13}+\sqrt{{x^2}-10x+29}$的最小值为2$\sqrt{5}$．

Answer 1

分析 由配方可得函数表示f（x）表示P（x，0）到两点A（3，2），B（5，2）的距离之和．作出点A关于x轴的对称点A'（3，-2），连接A'B，交x轴于P，运用两点之间线段最短，由两点的距离公式计算即可得到．

解答 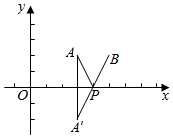解：函数f（x）$\sqrt{{x}^{2}-6x+13}$+$\sqrt{{x}^{2}-10x+29}$
=$\sqrt{（x-3）^{2}+{2}^{2}}$+$\sqrt{（x-5）^{2}+{2}^{2}}$，
设点P（x，0），A（3，2），B（5，2），
则f（x）表示P到两点A，B的距离之和．
作出点A关于x轴的对称点A'（3，-2），
连接A'B，交x轴于P，
则||PA|+|PB|=|PA'|+|PB|≥|A'B|
=$\sqrt{（5-3）^{2}+（2+2）^{2}}$=2$\sqrt{5}$，
则当A，P，B'三点共线，取得最小值2$\sqrt{5}$．
故答案为：2$\sqrt{5}$．

点评 本题考查函数的最值的求法，注意运用几何方法：对称法，两点间的距离公式，属于中档题．