
分析 ①数列{an}的前n项和Sn=100n-n2(n∈N*),当n=1时,a1=S1=99;当n≥2时,an=Sn-Sn-1,可得an=101-2n,是关于n的一次函数,即可证明.
②bn=|an|=|101-2n|=$\left\{\begin{array}{l}{101-2n,n≤50}\\{2n-101,n≥51}\end{array}\right.$,对n分类讨论,利用等差数列的前n项和公式即可得出.
解答 ①证明:∵数列{an}的前n项和Sn=100n-n2(n∈N*),∴当n=1时,a1=S1=99;
当n≥2时,an=Sn-Sn-1=100n-n2-[100(n-1)-(n-1)2]=101-2n,当n=1时,上式也成立.
∴an=101-2n,是关于n的一次函数,因此是等差数列.
②解:bn=|an|=|101-2n|=$\left\{\begin{array}{l}{101-2n,n≤50}\\{2n-101,n≥51}\end{array}\right.$,
∴当n≤50时,数列{bn}的前n项和Tn=Sn=100n-n2.
当n≥51时,数列{bn}的前n项和Tn=(a1+a2+…+a50)-(a51+a52+…+an)
=2S50-Sn
=2(100×50-502)-(100n-n2)
=n2-100n+5000.
∴Tn=$\left\{\begin{array}{l}{100n-{n}^{2},n≤50}\\{{n}^{2}-100n+5000,n≥51}\end{array}\right.$.
点评 本题考查了等差数列的定义通项公式及其前n项和公式、绝对值数列求和问题,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
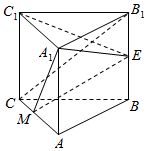 如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.
如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
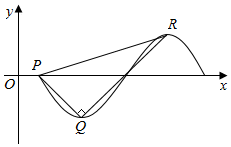 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )
f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 320 | B. | 360 | C. | 384 | D. | 390 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com