
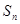 是各项均为非零实数的数列
是各项均为非零实数的数列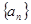 的前
的前 项和,给出如下两个命题上:
项和,给出如下两个命题上: :
: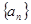 是等差数列;命题
是等差数列;命题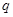 :等式
:等式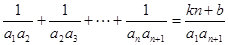 对任意
对任意 (
(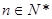 )恒成立,其中
)恒成立,其中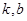 是常数。
是常数。 是
是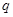 的充分条件,求
的充分条件,求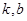 的值;
的值;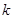 与
与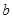 ,问
,问 是否为
是否为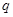 的必要条件,请说明理由;
的必要条件,请说明理由; 为真命题,对于给定的正整数
为真命题,对于给定的正整数 (
(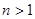 )和正数M,数列
)和正数M,数列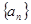 满足条件
满足条件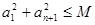 ,试求
,试求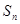 的最大值。
的最大值。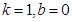 ;(2)是,证明见解析;(3)
;(2)是,证明见解析;(3)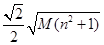 .
.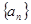 是等差数列,和
是等差数列,和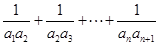 可以用裂项相消法求出,等式
可以用裂项相消法求出,等式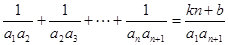 就变为关于
就变为关于 的恒等式,利用恒等式的知识可求出
的恒等式,利用恒等式的知识可求出 ;(2)等式
;(2)等式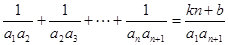 对任意
对任意 (
(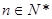 )恒成立,等式左边是一个和式,相当于一个新数列的前
)恒成立,等式左边是一个和式,相当于一个新数列的前 项和,处理方法是把式子中的
项和,处理方法是把式子中的 用
用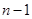 代换后,两式相减,本题中得到
代换后,两式相减,本题中得到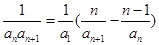 ,这个式子可整理为
,这个式子可整理为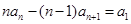 ,这是关于
,这是关于 的恒等式,因此
的恒等式,因此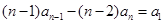
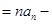
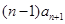 ,即
,即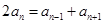 , 这就说明
, 这就说明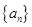 为等差数列,得证,解题时还要注意对
为等差数列,得证,解题时还要注意对 的初始值是否成立;(3)已知条件为等差数列
的初始值是否成立;(3)已知条件为等差数列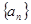 中
中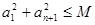 ,要求
,要求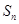 的最大值,为了能对数列
的最大值,为了能对数列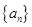 进行处理,我们利用三角换元法,对已知条件变换,设设
进行处理,我们利用三角换元法,对已知条件变换,设设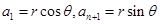 ,(
,(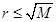 ),这样数列的公差
),这样数列的公差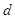 就可求出,从而也就能求出前
就可求出,从而也就能求出前 项和
项和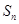 ,
,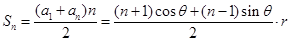 ,再利用三角函数
,再利用三角函数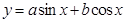 的最大值为
的最大值为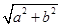 ,就能求出
,就能求出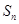 的最大值.
的最大值.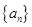 的公差为
的公差为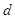 ,则原等式可化为
,则原等式可化为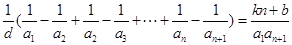 ,所以
,所以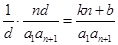 ,
,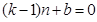 对于
对于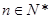 恒成立,所以
恒成立,所以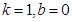 . 4分
. 4分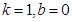 时,假设
时,假设 为
为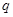 的必要条件,即“若
的必要条件,即“若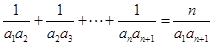 ①对于任意的
①对于任意的 (
(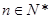 )恒成立,则
)恒成立,则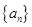 为等差数列”,
为等差数列”,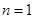 时,
时,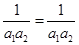 显然成立, 6分
显然成立, 6分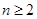 时,
时,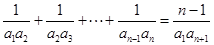 ②,由①-②得:
②,由①-②得: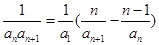 ,
,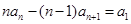 ③,
③,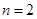 时,
时,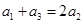 ,即
,即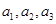 成等差数列,
成等差数列,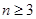 时,
时,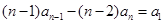 ④,由③④得
④,由③④得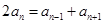 ,所以
,所以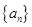 为等差数列,即
为等差数列,即 是
是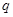 的必要条件. 10分
的必要条件. 10分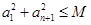 ,可设
,可设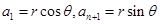 ,所以
,所以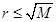 .
.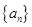 的公差为
的公差为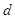 ,则
,则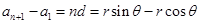 ,所以
,所以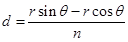 ,
,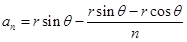 ,
,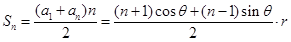
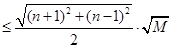
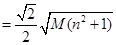 ,
,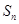 的最大值为
的最大值为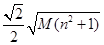 . 16分
. 16分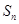 的最大值问题.
的最大值问题.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com