Question

4．F₁，F₂分别为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的左右焦点，P为椭圆上一动点，F₂关于直线PF₁的对称点为M，F₁关于直线PF₂的对称点为N，则当|MN|最大时，S${\;}_{△P{F}_{1}{F}_{2}}$为（　　）

• A． 2
• B． $\sqrt{2}$
• C． $\frac{2\sqrt{3}}{3}$
• D． $\frac{\sqrt{3}}{3}$

Answer 1

分析 由题意画出图形，得到当P，M，N共线时，|MN|最大，由此可知∠F₁PF₂=60°，然后利用余弦定理求得$|P{F}_{1}||P{F}_{2}|=\frac{8}{3}$．再代入三角形面积公式得答案．

解答 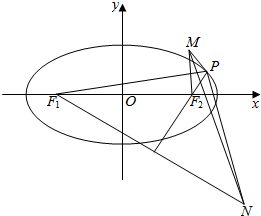解：由$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1，得a²=4，b²=2，则c²=a²-b²=2，
∴${F}_{1}（-\sqrt{2}，0），{F}_{2}（\sqrt{2}，0）$，
连接PM，PN，
∵|PM|+|PN|=|PF₁|+|PF₂|=2a，
∴当P，M，N共线时，|MN|最大，
此时∠MPF₁=∠F₁PF₂，∠F₁PF₂=∠F₂PN，
由∠MPF₁+∠F₁PF₂+F₂PN=180°，
得∠F₁PF₂=60°，
在△F₁PF₂中，由余弦定理可得：
$4{c}^{2}=|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-2|P{F}_{1}||P{F}_{2}|cos60°$，
∴$8=（|P{F}_{1}|+|P{F}_{2}|）^{2}-3|P{F}_{1}||P{F}_{2}|$，
即$|P{F}_{1}||P{F}_{2}|=\frac{8}{3}$．
∴S${\;}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}×\frac{8}{3}×\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}$．
故选：C．

点评 本题考查椭圆的简单性质，考查了数形结合的解题思想方法和数学转化思想方法，属中档题．