
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() ,
,
(1)求函数f(x)的定义域;
(2)求f(﹣1),f(12)的值.
【答案】
(1)解:要使函数的有意义,则 ![]() ,
,
即 ![]() ,所以x≥﹣4且x≠1.
,所以x≥﹣4且x≠1.
所以函数的定义域为{x|x≥﹣4且x≠1}
(2)解: ![]() ,
,
![]()
【解析】(1)利用根式函数和分式函数的定义域求法求函数的定义域.(2)利用函数关系式直接代入求值.
【考点精析】关于本题考查的函数的定义域及其求法和函数的值,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点. 
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)求点A到平面PMB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(1)设p:实数x满足(x﹣3a)(x﹣a)<0,其中a>0,q:实数x满足 ![]() ,若p是q的充分不必要条件,求实数a的取值范围;
,若p是q的充分不必要条件,求实数a的取值范围;
(2)设命题p:“函数 ![]() 无极值”;命题q:“方程
无极值”;命题q:“方程 ![]() 表示焦点在y轴上的椭圆”,若p或q为真命题,p且q为假命题,求实数m的取值范围.
表示焦点在y轴上的椭圆”,若p或q为真命题,p且q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1),g(x)=loga(1﹣x)其中(a>0且a≠1).
(1)判断f(x)﹣g(x)的奇偶性,并说明理由;
(2)求使f(x)﹣g(x)>0成立的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆锥![]() 和圆柱
和圆柱![]() 的组合体(它们的底面重合),圆锥的底面圆
的组合体(它们的底面重合),圆锥的底面圆![]() 半径为
半径为![]() ,
, ![]() 为圆锥的母线,
为圆锥的母线, ![]() 为圆柱
为圆柱![]() 的母线,
的母线, ![]() 为下底面圆
为下底面圆![]() 上的两点,且
上的两点,且![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线为
的准线为![]() ,焦点为
,焦点为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求过点![]() ,且与
,且与![]() 相切的圆的方程;
相切的圆的方程;
(2)过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,
两点, ![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过
经过![]() 、
、![]() ,圆心
,圆心![]() 在直线
在直线![]() 上,过点
上,过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 交圆相交于
交圆相交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)(i)请问![]() 是否为定值.若是,请求出该定值,若不是,请说明理由;
是否为定值.若是,请求出该定值,若不是,请说明理由;
(ii)若![]() 为坐标原点,且
为坐标原点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车入住泉州一周年以来,因其“绿色出行,低碳环保”的理念而备受人们的喜爱,值此周年之际,某机构为了了解共享单车使用者的年龄段,使用频率、满意度等三个方面的信息,在全市范围内发放![]() 份调查问卷,回收到有效问卷
份调查问卷,回收到有效问卷![]() 份,现从中随机抽取
份,现从中随机抽取![]() 份,分别对使用者的年龄段、
份,分别对使用者的年龄段、![]() ~
~![]() 岁使用者的使用频率、
岁使用者的使用频率、![]() ~
~![]() 岁使用者的满意度进行汇总,得到如下三个表格:
岁使用者的满意度进行汇总,得到如下三个表格:
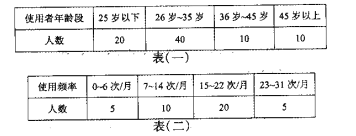
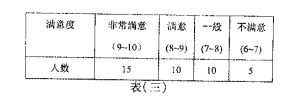
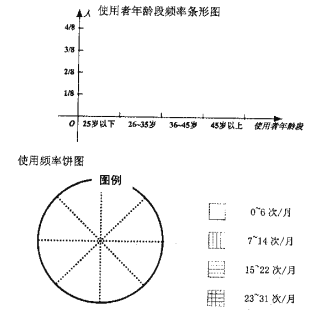
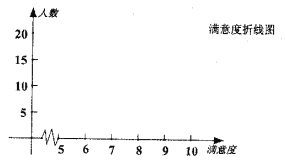
(Ⅰ)依据上述表格完成下列三个统计图形:
(Ⅱ)某城区现有常住人口![]() 万,请用样本估计总体的思想,试估计年龄在
万,请用样本估计总体的思想,试估计年龄在![]() 岁~
岁~![]() 岁之间,每月使用共享单车在
岁之间,每月使用共享单车在![]() ~
~![]() 次的人数.
次的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com