
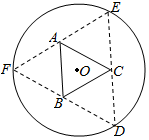
 如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.
如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3. 分析 由题,连接OD,交BC于点G,由题意得OD⊥BC,OG=$\frac{\sqrt{3}}{6}$BC,设OG=x,则BC=2$\sqrt{3}$x,DG=5-x,三棱锥的高h=$\sqrt{25-10x}$,求出S△ABC=3$\sqrt{3}{x}^{2}$,V=$\frac{1}{3}{S}_{△ABC}×h$=$\sqrt{3}•\sqrt{25{x}^{4}-10{x}^{5}}$,令f(x)=25x4-10x5,x∈(0,$\frac{5}{2}$),f′(x)=100x3-50x4,f(x)≤f(2)=80,由此能求出体积最大值.
解答 解:由题意,连接OD,交BC于点G,由题意得OD⊥BC,OG=$\frac{\sqrt{3}}{6}$BC,
即OG的长度与BC的长度成正比,
设OG=x,则BC=2$\sqrt{3}$x,DG=5-x,
三棱锥的高h=$\sqrt{D{G}^{2}-O{G}^{2}}$=$\sqrt{25-10x+{x}^{2}-{x}^{2}}$=$\sqrt{25-10x}$,
${S}_{△ABC}=\frac{1}{2}×\frac{\sqrt{3}}{2}×(2\sqrt{3}x)^{2}$=3$\sqrt{3}{x}^{2}$,
则V=$\frac{1}{3}{S}_{△ABC}×h$=$\sqrt{3}{x}^{2}×\sqrt{25-10x}$=$\sqrt{3}•\sqrt{25{x}^{4}-10{x}^{5}}$,
令f(x)=25x4-10x5,x∈(0,$\frac{5}{2}$),f′(x)=100x3-50x4,
令f′(x)≥0,即x4-2x3≤0,解得x≤2,
则f(x)≤f(2)=80,
∴V≤$\sqrt{3}×\sqrt{80}$=4$\sqrt{15}$cm3,∴体积最大值为4$\sqrt{15}$cm3.
故答案为:4$\sqrt{15}$cm3.
点评 本题考查三棱锥的体积的最大值的求法,考查空间中线线、线面、面面间的位置关系、函数性质、导数等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,是中档题.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
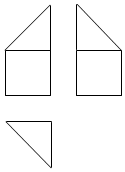 某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1033 | B. | 1053 | C. | 1073 | D. | 1093 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
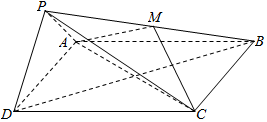 如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=$\sqrt{6}$,AB=4.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=$\sqrt{6}$,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com