
分析 (1)通过对f(x)=x3+ax2+bx+1求导可知g(x)=f′(x)=3x2+2ax+b,进而再求导可知g′(x)=6x+2a,通过令g′(x)=0进而可知f′(x)的极小值点为x=-$\frac{a}{3}$,从而f(-$\frac{a}{3}$)=0,整理可知b=$\frac{2{a}^{2}}{9}$+$\frac{3}{a}$(a>0),结合f(x)=x3+ax2+bx+1(a>0,b∈R)有极值可知f′(x)=0有两个不等的实根,进而可知a>3.
(2)通过(1)构造函数h(a)=b2-3a=$\frac{4{a}^{4}}{81}$-$\frac{5a}{3}$+$\frac{9}{{a}^{2}}$=$\frac{1}{81{a}^{2}}$(4a3-27)(a3-27),结合a>3可知h(a)>0,从而可得结论;
(3)通过(1)可知f′(x)的极小值为f′(-$\frac{a}{3}$)=b-$\frac{{a}^{2}}{3}$,利用韦达定理及完全平方关系可知y=f(x)的两个极值之和为$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2,进而问题转化为解不等式b-$\frac{{a}^{2}}{3}$+$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2=$\frac{3}{a}$-$\frac{{a}^{2}}{9}$≥-$\frac{7}{2}$,因式分解即得结论.
解答 (1)解:因为f(x)=x3+ax2+bx+1,
所以g(x)=f′(x)=3x2+2ax+b,g′(x)=6x+2a,
令g′(x)=0,解得x=-$\frac{a}{3}$.
由于当x>-$\frac{a}{3}$时g′(x)>0,g(x)=f′(x)单调递增;当x<-$\frac{a}{3}$时g′(x)<0,g(x)=f′(x)单调递减;
所以f′(x)的极小值点为x=-$\frac{a}{3}$,
由于导函数f′(x)的极值点是原函数f(x)的零点,
所以f(-$\frac{a}{3}$)=0,即-$\frac{{a}^{3}}{27}$+$\frac{{a}^{3}}{9}$-$\frac{ab}{3}$+1=0,
所以b=$\frac{2{a}^{2}}{9}$+$\frac{3}{a}$(a>0).
因为f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,
所以f′(x)=3x2+2ax+b=0的实根,
所以4a2-12b≥0,即a2-$\frac{2{a}^{2}}{3}$+$\frac{9}{a}$≥0,解得a≥3,
所以b=$\frac{2{a}^{2}}{9}$+$\frac{3}{a}$(a≥3).
(2)证明:由(1)可知h(a)=b2-3a=$\frac{4{a}^{4}}{81}$-$\frac{5a}{3}$+$\frac{9}{{a}^{2}}$=$\frac{1}{81{a}^{2}}$(4a3-27)(a3-27),
由于a>3,所以h(a)>0,即b2>3a;
(3)解:由(1)可知f′(x)的极小值为f′(-$\frac{a}{3}$)=b-$\frac{{a}^{2}}{3}$,
设x1,x2是y=f(x)的两个极值点,则x1+x2=$-\frac{2a}{3}$,x1x2=$\frac{b}{3}$,
所以f(x1)+f(x2)=${{x}_{1}}^{3}$+${{x}_{2}}^{3}$+a(${{x}_{1}}^{2}$+${{x}_{2}}^{2}$)+b(x1+x2)+2
=(x1+x2)[(x1+x2)2-3x1x2]+a[(x1+x2)2-2x1x2]+b(x1+x2)+2
=$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2,
又因为f(x),f′(x)这两个函数的所有极值之和不小于-$\frac{7}{2}$,
所以b-$\frac{{a}^{2}}{3}$+$\frac{4{a}^{3}}{27}$-$\frac{2ab}{3}$+2=$\frac{3}{a}$-$\frac{{a}^{2}}{9}$≥-$\frac{7}{2}$,
因为a>3,所以2a3-63a-54≤0,
所以2a(a2-36)+9(a-6)≤0,
所以(a-6)(2a2+12a+9)≤0,
由于a>3时2a2+12a+9>0,
所以a-6≤0,解得a≤6,
所以a的取值范围是(3,6].
点评 本题考查利用导数研究函数的单调性、极值,考查运算求解能力,考查转化思想,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
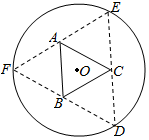 如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.
如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为4$\sqrt{15}$cm3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com