
将正整数按如图的规律排列,把第一行数1,2,5,10,17, 记为数列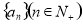 ,第一
,第一
数列1,4,9,16,25, 记为数列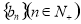

(1)写出数列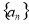 ,
,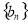 的通项公式;
的通项公式;
(2)若数列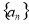 ,
,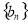 的前n项和分别为
的前n项和分别为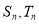 ,用数学归纳法证明:
,用数学归纳法证明: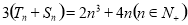 ;
;
(3)当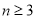 时,证明:
时,证明: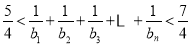 .
.
(1)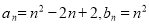 ;(2)证明略;(3)证明略.
;(2)证明略;(3)证明略.
【解析】
试题分析:(1)数学归纳法是一种重要的数学思想方法,主要用于解决与正整数有关的数学问题,用数学归纳法证明等式问题,要“先看项”,弄清等式两边的构成规律,等式两边各有多少项,初始值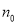 是多少;(2)由
是多少;(2)由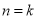 时等式成立,推出
时等式成立,推出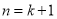 时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写;(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.
时等式成立,一要找出等式两边的变化(差异),明确变形目标;二要充分利用归纳假设,进行合理变形,正确写出证明过程,由于“猜想”是“证明”的前提和“对象”,务必保证猜想的正确性,同时必须严格按照数学归纳法的步骤书写;(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.
试题解析:【解析】
(1)由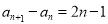 ,得:
,得: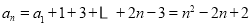 , 3分
, 3分
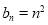 . 4分
. 4分
① 当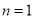 时,
时,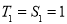 ,∴
,∴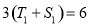 ,又
,又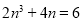 ,∴
,∴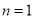 时等式成立; 5分
时等式成立; 5分
② 假设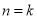 时等式成立,即
时等式成立,即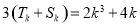 ,
,
则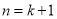 时,
时,
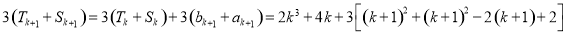
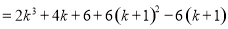
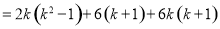
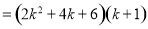
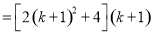
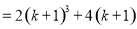 ,
,
∴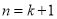 时等式也成立. 8分
时等式也成立. 8分
根据①②,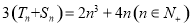 都成立. 9分
都成立. 9分
(3)当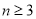 时,
时,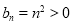 ,∴
,∴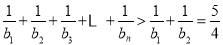 . 11分
. 11分
又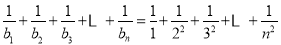
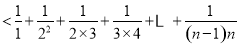
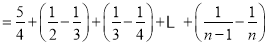
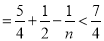 .
.
综上可知: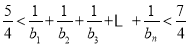 成立. 14分
成立. 14分
考点:(1)求数列的通项公式;(2)用数学归纳法证明命题;(3)裂项法求数列的和.


科目:高中数学 来源:2015届广东省广州市高三上学期第一次质量检测文科数学试卷(解析版) 题型:选择题
已知各项为正的等比数列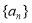 满足
满足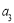 ·
·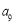 =
=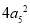 ,
,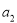 =1,则
=1,则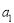 = ( )
= ( )
A.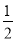 B.2 C.
B.2 C.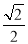 D.
D.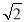
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:解答题
已知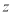 是复数,若
是复数,若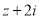 为实数(
为实数(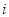 为虚数单位),且
为虚数单位),且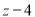 为纯虚数.
为纯虚数.
(1)求复数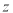 ;
;
(2)若复数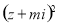 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数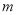 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com