
分析 (1)先求f′(0)与f′(1),看两值是否异号,然后证明f′(x)在[0,1]上单调性,即可证明函数f(x)在区间[0,1]上存在唯一的极值点;
(2)由题意得到ex-$\frac{1}{2}$x2-ax-1≥0,构造g(x)=ex-$\frac{1}{2}$x2-ax-1,分类讨论求出g(x)的最值,即可得到a的范围.
解答 解:(1)∵f′(0)=e0-3=-2<0,f′(1)=e+1>0,
∴f′(0)•f′(1)<0,
令h(x)=f′(x)=ex+4x-3,则h′(x)=ex+4>0,
∴f′(x)在[0,1]上单调递增,
∴f′(x)在[0,1]上存在唯一零点,
∴f(x)在[0,1]上存在唯一的极值点
(2)由 f(x)≥$\frac{5}{2}$x3+(a-3)x+1,
得ex+2x2-3x≥$\frac{5}{2}$x3+(a-3)x+1
∴ex-$\frac{1}{2}$x2-ax-1≥0,
令g(x)=ex-$\frac{1}{2}$x2-ax-1,x≥0,
则g(0)=0,g′(x)=ex-x-a,
令h(x)=ex-x-a,
则h′(x)=ex-1,
∵x≥0,
∴h′(x)≥0,
∴h(x)在[0,+∞)上单调递增,
∴h(x)≥h(0)=1-a,
①当a≤1时,h(x)≥0恒成立,即g′(x)≥0,
∴g(x)在[0,+∞)上单调递增,
∴g(x)≥g(0)=0,
②当a>1时,存在x0∈[0,+∞),使h(x0)=0,即g′(x0)=0,
当x∈[0,x0)时,g′(x)<0,
∴g(x)在[0,x0)上单调递减,
∴g(x)<g(0)=0,这与g(x)≥0在[0,+∞)上恒成立矛盾,
综上所示a≤1.
点评 本题主要考查了利用导数求闭区间上函数的最值,以及函数恒成立问题等基础题知识,考查运算求解能力、推理论证能力,化归与转化思想,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
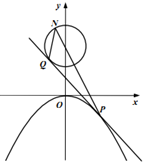 如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.
如图,曲线C1:x2=-4y,曲线C2:x2+(y-m)2=1(m>0),过曲线C1上的一点P(2,-1)作曲线C1的切线l,且l与C2恰好相切,切点为Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 95% | B. | 99% | C. | 97.5% | D. | 90% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(b)>bf(a) | B. | af(a)>bf(b) | C. | bf(a)>af(b) | D. | bf(b)>af(a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com