Question

3．如图，正方体ABCD-A₁B₁C₁D₁的棱长为4，P为BC的中点，Q为线段CC₁上的动点（异于C点），过点A、P、Q的平面截面记为M．
则当CQ∈（0，2]时（用区间或集合表示），M为四边形；　
当CQ=2时（用数值表示），M为等腰梯形；
当CQ=4时，M的面积为8$\sqrt{6}$．

Answer 1

分析 作出图形，可分析出当CQ∈（0，2]时，M为四边形；当Q为CC₁的中点时M为等腰梯形；当CQ=4时，取A₁D₁的中点F，可知截面为APC₁F为菱形，从而可求M的面积．

解答 解：∵CC₁=4，∴当CQ∈（0，2]时，M为四边形（见图）；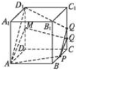

当Q为CC₁的中点，即CQ=2时，PQ∥AD₁，AP=QD₁=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$，
M为等腰梯形APQD₁；
当CQ=4时，Q与C₁重合（如图），

取A₁D₁的中点F，连接AF，C₁F，AP，PC₁，则PC₁∥AF，且PC₁=AF，
所以截面为APC₁F为菱形，故其面积为：S=$\frac{1}{2}$AC₁•PF=$\frac{1}{2}$×4$\sqrt{3}$×4$\sqrt{2}$=8$\sqrt{6}$．
故答案为：（0，2]；2；8$\sqrt{6}$．

点评 本题考查棱柱的结构特征，考作出图形是分析解决问题的关键，查作图与推理能力运算能力，属于中档题．