
分析 (1)由椭圆性质求出A(-1,0),B(1,0).由题意知双曲线的焦距2c=2 $\sqrt{5}$,实半轴a=1,由此能求出双曲线C的方程.
(2)设点P(x1,y1),T(x2,y2)(x1>0,x2>0),则直线AP的方程为y=k(x+1),代入x2+$\frac{{y}^{2}}{4}$=1,得(4+k2)x2+2k2x+k2-4=0,由此能证明为x1•x2为定值.
(3)由已知条件推导出x12+y12≤16,x12≤4,从而得到1<x1≤2,由此能求出S12-S22的取值范围为[0,1].
解答 (1)解:∵椭圆x2+$\frac{{y}^{2}}{4}$=1的左、右两个顶点分别为A,B,
∴A(-1,0),B(1,0).
∵曲线C是以A,B两点为顶点,焦距为2$\sqrt{5}$的双曲线,
∴双曲线的焦距2c=2$\sqrt{5}$,实半轴a=1,
∴c=$\sqrt{5}$,b2=c2-a2=4.
∴双曲线C的方程为x2-$\frac{{y}^{2}}{4}$=1.
(2)证明:设点P(x1,y1),T(x2,y2)(x1>0,x2>0),
直线AP的斜率为k(k>0),则直线AP的方程为y=k(x+1),
代入x2+$\frac{{y}^{2}}{4}$=1,
整理,得(4+k2)x2+2k2x+k2-4=0,
解得x=-1或x=$\frac{4-{k}^{2}}{4+{k}^{2}}$,
所以x2=$\frac{4-{k}^{2}}{4+{k}^{2}}$.
同理将直线方程代入x2-$\frac{{y}^{2}}{4}$=1,解得x1=$\frac{4+{k}^{2}}{4-{k}^{2}}$.
∴x1x2=$\frac{4+{k}^{2}}{4-{k}^{2}}$•$\frac{4-{k}^{2}}{4+{k}^{2}}$=1为定值.
(3)解:由(2)知,$\overrightarrow{PA}$=(-1-x1,-y1),$\overrightarrow{PB}$=(1-x1,-y1),
又$\overrightarrow{PA}$•$\overrightarrow{PB}$≤15,
∴(-1-x1)(1-x1)+y12≤15,即 x12+y12≤16,
∵点P在双曲线上,则 x12-$\frac{{{y}_{1}}^{2}}{4}$=1,
∴x12+4 x12-4≤16,即 x12≤4,
又点P是双曲线在第一象限内的点,∴1<x1≤2,
∵s1=$\frac{1}{2}$|AB||y2|=|y2|,s2=$\frac{1}{2}$|OB||y1|=$\frac{1}{2}$|y1|,
所以.S12-S22=y22-$\frac{1}{4}$y12=(4-4x22 )-( x12-1)=5-x12-4x22
由(Ⅱ)知x1•x2=1,即,x2=$\frac{1}{{x}_{1}}$,
设t=x12,则1<t≤4,
∴S12-S22=5-t-$\frac{4}{t}$,
∵t+$\frac{4}{t}$在(1,2]上单调递减,在[2,4]上单调递增,
∴当t=4,即x1=2时,(S12-S22)min=0.
当t=2,即x1=$\sqrt{2}$.(S12-S22)max=1
∴S12-S22的取值范围为[0,1].
点评 本题考查曲线方程的求法,考查两数乘积为定值的证明,考查两三角形面积的平方差的取值范围的求法,解题时要注意函数与方程思想的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,直四棱柱ABCD-A1B1C1D1内接于半径为$\sqrt{3}$的半O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长为2.
如图所示,直四棱柱ABCD-A1B1C1D1内接于半径为$\sqrt{3}$的半O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长为2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
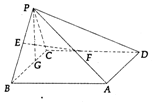 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com