
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
分析 利用裂项法进行求和即可.
解答 解:∵数列{an}的通项公式是an=$\frac{1}{n(n+1)}$,
∴an=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
则前n项和公式Sn=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$,
由Sn=1-$\frac{1}{n+1}$=$\frac{2014}{2015}$,
得$\frac{1}{n+1}$=1-$\frac{2014}{2015}$=$\frac{1}{2015}$,
即n+1=2015,
则n=2014,
故选:C
点评 本题主要考查及数列求和的应用,利用裂项法是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | (-$\sqrt{3}$,2] | C. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] | D. | [-$\sqrt{3}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
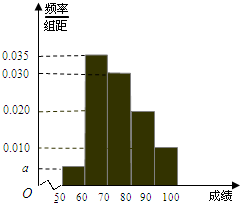 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com