
| A. | 2n-1 | B. | $\sqrt{\frac{{4}^{n}-1}{3}}$ | C. | $\frac{{2}^{n}-1}{3}$ | D. | $\frac{{2}^{n+1}-3}{3}$ |
分析 由等比数列{an}的前n项和求出首项和公比,进一步得到数列{$\sqrt{{a}_{n}}$}的首项和公比,再由等比数列的前n项和得答案.
解答 解:由Sn=$\frac{{4}^{n}-1}{3}$,得a1=S1=1;
当n≥2时,an=Sn-Sn-1=$\frac{{4}^{n}-1}{3}-\frac{{4}^{n-1}-1}{3}$=4n-1.
验证a1=1适合上式,
∴${a}_{n}={4}^{n-1}$,则等比数列{an}的公比q=$\frac{{a}_{n+1}}{{a}_{n}}=\frac{{4}^{n}}{{4}^{n-1}}=4$.
∴数列{$\sqrt{{a}_{n}}$}的首项为$\sqrt{{a}_{1}}=1$,公比为2.
∴数列{$\sqrt{{a}_{n}}$}的前n项和Tn=$\frac{1×(1-{2}^{n})}{1-2}={2}^{n}-1$.
故选:A.
点评 本题考查等比数列的前n项和,考查等比关系的确定,是中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
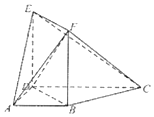 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2,AD=AB=1,四边形BDEF为正方形,且平面BDEF丄平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | 2 | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com