
| a |
| b |
| a |
| b |
| 3 |
| A、3 | ||
B、
| ||
C、2
| ||
D、
|
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 3 |
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 3 |
x2+y2+2xy×
|
| 3 |
| 3 |
| 3 |


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
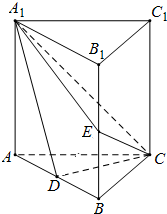 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、21π | ||||
| B、12π | ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、若|
| ||||||||||||||
B、若
| ||||||||||||||
C、若(
| ||||||||||||||
D、若
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 某厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )| A、45 | B、60 | C、75 | D、90 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com