
分析 (I)利用余弦定理即可得出;
(II)利用倍角公式、和差公式可得:f(x)=$sin(x+\frac{π}{6})$+$\frac{1}{2}$,再利用三角函数的单调性与值域可得B,进而得出三角形的面积.
解答 解:(Ⅰ)在△ABC中,∵b2+c2-a2=bc,
由余弦定理 a2=b2+c2-2bccosA 可得cosA=$\frac{1}{2}$.
∵0<A<π,
∴A=$\frac{π}{3}$.
(Ⅱ)f(x)=$\sqrt{3}$sin$\frac{x}{2}$cos$\frac{x}{2}$+cos2$\frac{x}{2}$=$\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx+\frac{1}{2}$=$sin(x+\frac{π}{6})$+$\frac{1}{2}$,
当x=B时,f(B)=$sin(B+\frac{π}{6})$+$\frac{1}{2}$,
∵A=$\frac{π}{3}$,∴B∈$(0,\frac{2π}{3})$,
∴$\frac{π}{6}$<$B+\frac{π}{6}$$<\frac{5π}{6}$,
∴当B+$\frac{π}{6}$=$\frac{π}{2}$时,即B=$\frac{π}{3}$时,f(B)有最大值是$\frac{3}{2}$.
又∵A=$\frac{π}{3}$,∴C=$\frac{π}{3}$.
∴△ABC为等边三角形.
∴S=$\frac{1}{2}{a^2}sin\frac{π}{3}=\sqrt{3}$.
点评 本题考查了余弦定理、倍角公式、和差公式、三角函数的单调性与值域、三角形的面积计算公式,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | (-4,2) | B. | (-∞,-4)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图是一次摄影大赛上7位评委给某参赛作品打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.
如图是一次摄影大赛上7位评委给某参赛作品打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
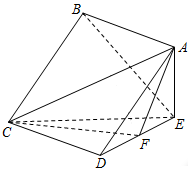 如图,在四棱锥E-ABCD中,底面ABCD是边长为$\sqrt{2}$的正方形,平面AEC⊥平面CDE,∠AEC=90°,F为DE中点,且DE=1.
如图,在四棱锥E-ABCD中,底面ABCD是边长为$\sqrt{2}$的正方形,平面AEC⊥平面CDE,∠AEC=90°,F为DE中点,且DE=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com