
 给定椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0).设t>0,过点T(0,t)斜率为k的 直线l与椭圆C交于M,N两点,O为坐标原点.
给定椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0).设t>0,过点T(0,t)斜率为k的 直线l与椭圆C交于M,N两点,O为坐标原点.分析 (Ⅰ)根据题意,设l方程为y=kx+t,联立直线与椭圆的方程可得(b2+a2k2)x2+2a2ktx+a2(t2-b2)=0;由根与系数的关系的关系表示|OT|和|xM-xN|,进而由三角形面积公式计算可得答案;
(Ⅱ)由(Ⅰ)可得S的表达式,分$t≥\frac{b}{{\sqrt{2}}}$与$0<t<\frac{b}{{\sqrt{2}}}$两种情况讨论,分析S的最大值,综合即可得答案.
解答 解:(Ⅰ)根据题意,设l方程为y=kx+t,
将l方程代入C方程整理得(b2+a2k2)x2+2a2ktx+a2(t2-b2)=0;
△=4a4k2t2-4a2(t2-b2)(b2+a2k2)=4a2b2(b2+a2k2-t2).
由△>0得k,t应满足的条件为 b2+a2k2-t2>0,
$S=\frac{1}{2}|{x_M}-{x_N}||OT|$=$\frac{1}{2}•\frac{{\sqrt{△}}}{{{b^2}+{a^2}{k^2}}}•t$=$\frac{{abt\sqrt{{b^2}+{a^2}{k^2}-{t^2}}}}{{{b^2}+{a^2}{k^2}}}$.
所以$S=\frac{{abt\sqrt{{b^2}+{a^2}{k^2}-{t^2}}}}{{{b^2}+{a^2}{k^2}}}$,其中b2+a2k2>t2
(Ⅱ)$S=\frac{{abt\sqrt{{b^2}+{a^2}{k^2}-{t^2}}}}{{{b^2}+{a^2}{k^2}}}$=$abt\sqrt{-{{(\frac{t}{{{b^2}+{a^2}{k^2}}}-\frac{1}{2t})}^2}+\frac{1}{{4{t^2}}}}$.
当$t≥\frac{b}{{\sqrt{2}}}$,即${t^2}≥\frac{b^2}{2}$,取$k=±\sqrt{\frac{{2{t^2}-{b^2}}}{a^2}}$,有$\frac{t}{{{b^2}+{a^2}{k^2}}}=\frac{1}{2t}$,得${S_{max}}=\frac{1}{2}ab$.
当$0<t<\frac{b}{{\sqrt{2}}}$,即$0<{t^2}<\frac{b^2}{2}$,b2+a2k2>2t2,有$\frac{t}{{{b^2}+{a^2}{k^2}}}≤\frac{t}{b^2}<\frac{1}{2t}$,
取k=0,得${S_{max}}=\frac{at}{b}\sqrt{{b^2}-{t^2}}$.
所以,当k变化时,S的最大值g(t)=$\left\{\begin{array}{l}{\frac{1}{2}ab,t≥\frac{b}{\sqrt{2}}}\\{\frac{at}{b}\sqrt{{b}^{2}-{t}^{2}},0<t<\frac{b}{\sqrt{2}}}\end{array}\right.$.
点评 本题考查椭圆的几何性质,涉及椭圆与直线的位置关系,关键是掌握椭圆的几何性质.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{13}$ | D. | $\sqrt{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,a?α,则a⊥β | B. | 若α⊥γ,β⊥γ,则α∥β | ||
| C. | 若α∥β,a?α,b?β,则a∥b | D. | 若m⊥α,m∥n,n∥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
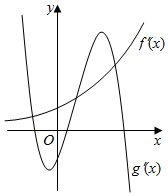 定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )
定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )| A. | 只有三个极大值点,无极小值点 | B. | 有两个极大值点,一个极小值点 | ||
| C. | 有一个极大值点,两个极小值点 | D. | 无极大值点,只有三个极小值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班别 | A | B | C | D |
| 人数 | 45 | 60 | 30 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com