考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)取BC1的中点F,证明MF⊥平面B1C1CB,利用平面与平面垂直的判定定理证明平面C1MB⊥平面B1C1MB;
(2)连接DB,C1B,可证∠C1BC就是平面C1MB与平面ABC所成二面角的平面角,在三角形C1BC中求出此角.
解答:
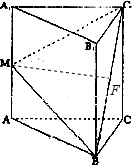
解:(1)证明:取BC
1的中点F,
∵正三棱柱ABC-A
1B
1C
1中,AB=AA
1=2,M为AA
1中点,
MB=MC
1,∴MF⊥BC1,MF⊥BB
1,BB
1∩BC
1=B,
∴MF⊥平面B
1C
1CB,MF?平面MBC
1,
∴平面C
1MB⊥平面B
1C
1MB.
(2)连接DB,C
1B,
则DB就是平面C
1MB与平面ABC的交线在△DCB中,
∵∠DBC=∠CBA+∠ABD=60°+30°=90°,
∴CB⊥DB,
又C
1C⊥平面CBD,
由三垂线定理得C
1B⊥DB,∴∠C
1BC就是平面C
1MB与平面ABC所成二面角的平面角(锐角),
∵侧面C
1B
1BC是正方形,∴∠C
1BC=45°,
故平面C
1MB与平面ABC所成的二面角(锐角)为45°.
点评:本题主要考查直线与平面的位置关系、棱柱等基本知识,考查空间想象能力、逻辑思维能力和运算能力.

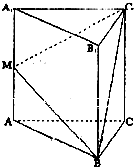 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M为AA1中点,求:
如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,M为AA1中点,求: 解:(1)证明:取BC1的中点F,
解:(1)证明:取BC1的中点F,

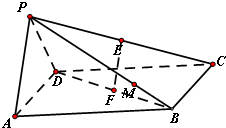 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,PA=PD=AD且侧面PAD⊥底面ABCD,若E、F分别为PC、BD的中点.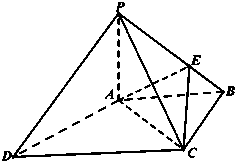 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=90°且PA=AB=BC,DC=2AB点E是棱PB上的动点.