练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．点P是双曲线$\frac{x^2}{9}$-$\frac{y^2}{16}$=1的右支上一点，M是圆（x+5）2+y2=4上一点，点N的坐标为（5，0），则|PM|-|PN|的最大值为（　　）
    A．5B．6C．7D．8

    分析 由题设通过双曲线的定义推出|PF1|-|PF2|=6，利用|MP|≤|PF1|+|MF1|，推出|PM|-|PN|≤|PF1|+|MF1|-|PF2|，求出最大值

    解答 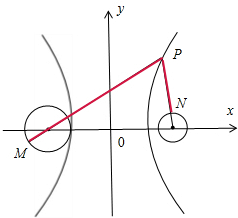解：双曲线$\frac{x^2}{9}$-$\frac{y^2}{16}$=1的右支中，∵a=3，b=4，c=5，
    ∴F1（-5，0），F2（5，0），
    ∵|PF1|-|PF2|=2a=6，
    ∴|MP|≤|PF1|+|MF1|，
    所以，|PM|-|PN|≤|PF1|+|MF1|-|PF2||
    =6+2
    =8．
    故选D

    点评 本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到轨迹方程的求法及直线与双曲线的相关知识，解题时要注意合理地进行等价转化

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．命题p：“?x≥0，e${\;}^{{x}_{0}}$＜x0+1”，则￢p是（　　）
    A．?x≥0，ex＜x+1B．?x≥0，ex＞x+1C．?x≥0，ex≥x+1D．?x≥0，ex≥x+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=$\sqrt{x+2}$+$\frac{1}{|x|-1}$．
    （1）求函数的定义域；     
    （2）求f（0），f[f（2）]的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．在极坐标系中，已知曲线C：ρ=2cosθ，将曲线C上的点向左平移一个单位，然后纵坐标不变，横坐标伸长到原来的2倍，得到曲线C1，又已知直线l：$\left\{\begin{array}{l}x=tcos\frac{π}{3}\\ y=\sqrt{3}+tsin\frac{π}{3}\end{array}$（t是参数），且直线l与曲线C1交于A，B两点．
    （1）求曲线C1的直角坐标方程，并说明它是什么曲线；
    （2）设定点P（0，$\sqrt{3}$），求$\frac{1}{|PA|}$+$\frac{1}{|PB|}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．集合A={x|x2+2x-3=0}，集合B={x|ax=3}，若A∩B=B，则实数a的值组成的集合为{0，-1，3}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知sinθ+cosθ=2sinα，sin2θ=2sin2β，则（　　）
    A．cosβ=2cosαB．cos2β=2cos2αC．cos2β+2cos2α=0D．cos2β=2cos2α

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=$\frac{{{x^2}-1}}{x}$-klnx（x≥1）．
    （1）若f（x）≥0恒成立，求k的取值范围；
    （2）若取$\sqrt{5}$=2.2361，试估计ln$\frac{5}{4}$的值．（ 精确到0.001）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知f（x）=$\frac{1}{x+2}$（x≠-2），h（x）=x2+1．
    （1）求f（2），h（1）的值；
    （2）求f[h（2）]的值；
    （3）求f（x），h（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某地区山体大面积滑坡，政府准备调运一批赈灾物资共装26辆车，从某市出发以v（km/h）的速度匀速直达灾区，如果两地公路长400km，且为了防止山体再次坍塌，每两辆车的间距保持在（$\frac{v}{20}$）2km．（车长忽略不计）设物资全部运抵灾区的时间为y小时，请建立y关于每车平均时速v（km/h）的函数关系式，并求出车辆速度为多少千米/小时，物资能最快送到灾区？

    查看答案和解析>>

    同步练习册答案