
分析 由二阶行列式展开式得到cos(75°-α)=$\frac{1}{3}$,再由诱导公式得cos(30°+2α)=cos[180°-2(75°-α)],由此利用二倍角公式能求出结果.
解答 解:∵$|{\begin{array}{l}{cos75°}&{-sinα}\\{sin75°}&{cosα}\end{array}}|=\frac{1}{3}$,
∴cos75°cosα+sin75°sinα=cos(75°-α)=$\frac{1}{3}$,
cos(30°+2α)=cos[180°-2(75°-α)]
=-cos[2(75°-α)]
=-[2cos2(75°-α)-1]
=-[2×$\frac{1}{9}$-1]
=$\frac{7}{9}$.
故答案为:$\frac{7}{9}$.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意二阶行列式展开式、诱导公式、倍角公式的性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
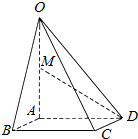 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
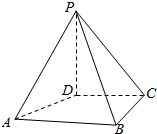 如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲、乙恰有一人的试跳成绩没有超过2米 | |
| B. | 甲、乙至少有一人的试跳成绩没有超过2米 | |
| C. | 甲、乙两人的试跳成绩都没有超过2米 | |
| D. | 甲、乙至少有一人的试跳成绩超过2米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com