
分析 (1)由题意列关于a,b,c的方程组,求解方程组得a,b的值,则椭圆方程可求;
(2)由(1)求出椭圆E.(i)设P(x0,y0),$\frac{{|{OQ}|}}{{|{OP}|}}=λ$,由题意知Q(-λx0,-λy0),把P,Q的坐标分别代入两椭圆方程,整体计算可得λ值;
(ii)设A(x1,y1),B(x2,y2),将y=kx+m代入椭圆E的方程,可得(1+4k2)x2+8kmx+4m2-16=0,利用弦长公式、点到直线的距离公式结合三角形面积公式列出△ABO的面积,利用换元法求其最大值,乘以3可得△ABQ面积的最大值.
解答 (1)解:由题意知$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}=1}\end{array}\right.$,解得:a2=4,b2=1.
∴椭圆C的标准方程为$\frac{x^2}{4}+{y^2}=1$;
(2)由(1)知椭圆E的方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$,
(i)证明:设P(x0,y0),$\frac{{|{OQ}|}}{{|{OP}|}}=λ$,由题意知Q(-λx0,-λy0),
∵$\frac{x_0^2}{4}+y_0^2=1$,又$\frac{{{{({-λ{x_0}})}^2}}}{16}+\frac{{{{({-λ{y_0}})}^2}}}{4}=1$,
∴$\frac{λ^2}{4}({\frac{x_0^2}{4}+y_0^2})=1$,得λ=2,即$\frac{{|{OQ}|}}{{|{OP}|}}=2$.
(ii)解:设A(x1,y1),B(x2,y2),将y=kx+m代入椭圆E的方程,
可得(1+4k2)x2+8kmx+4m2-16=0,
由△>0,可得m2<4+16k2…①
则有${x_1}+{x_2}=-\frac{8km}{{1+4{k^2}}},{x_1}{x_2}=\frac{{4{m^2}-16}}{{1+4{k^2}}}$,
∴$|{{x_1}-{x_2}}|=\frac{{4\sqrt{16{k^2}+4-{m^2}}}}{{1+4{k^2}}}$,
∵直线y=kx+m与轴交点的坐标为(0,m),
∴△OAB的面积$S=\frac{1}{2}|m|•|{{x_2}-{x_2}}|=\frac{{2\sqrt{16{k^2}+4-{m^2}}|m|}}{{1+4{k^2}}}$=$\frac{{2\sqrt{(16{k^2}+4-{m^2})•{m^2}}}}{{1+4{k^2}}}=2\sqrt{({4-\frac{m^2}{{1+4{k^2}}}})•\frac{m^2}{{1+4{k^2}}}}$,
令$\frac{m^2}{{1+4{k^2}}}=t$,将y=kx+m代入椭圆C的方程可得(1+4k2)x2+8kmx+4m2-4=0,
由△≥0,可得m2≤1+4k2…②
由①②可知0<t≤1,
因此$S=2\sqrt{({4-t})t}=2\sqrt{-{t^2}+4t}$,故$S≤2\sqrt{3}$,当且仅当t=1,即m2=1+4k2时取得最大值$2\sqrt{3}$.
由(i)知,△ABQ面积为3S,∴△ABQ面积的最大值为$6\sqrt{3}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了利用换元法求最值,是压轴题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:选择题
| A. | x-2y+5=0 | B. | 2x-y+5=0 | C. | x+2y+5=0 | D. | 2x+y+5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
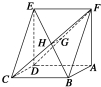 如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
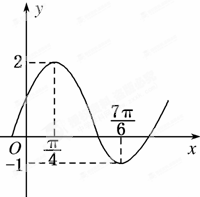 将函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,0<φ<π)的图象向右平移$\frac{2π}{3}$个单位,所得曲线的一部分如图所示,则f(x)的解析式为( )
将函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,0<φ<π)的图象向右平移$\frac{2π}{3}$个单位,所得曲线的一部分如图所示,则f(x)的解析式为( )| A. | f(x)=$\frac{3}{2}$sin($\frac{12}{11}$x-$\frac{21π}{22}$)+1 | B. | f(x)=$\frac{3}{2}$sin($\frac{12}{11}$x+$\frac{21π}{22}$)+$\frac{1}{2}$ | ||
| C. | f(x)=2sin($\frac{11}{12}$x+$\frac{21π}{22}$)-$\frac{1}{2}$ | D. | f(x)=$\frac{3}{2}$sin($\frac{12}{11}$x+$\frac{5π}{22}$)+$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com