练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知某蔬菜商店买进的土豆x（吨）与出售天数y（天）之间的关系如表所示：
    x234567912
    y12334568

    （Ⅰ）请根据表中数据在所给网格中绘制散点图；
    （Ⅱ）请根据表中提供的数据，用最小二乘法求出y关于x的线性回归方程$\widehaty=\widehatbx+\widehata$（其中$\widehatb$保留2位有效数字）；
    （Ⅲ）根据（Ⅱ）中的计算结果，若该蔬菜商店买进土豆40吨，则预计可以销售多少天（计算结果保留整数）？
    附：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$，$\widehata=\overline y-\widehatb\overline x$．

    分析 （Ⅰ）根据表中数据画出散点图即可；
    （Ⅱ）依题意，计算$\overline x$、$\overline y$，求出回归系数，写出回归直线方程；
    （Ⅲ）由回归方程计算x=40时y的值即可．

    解答 解：（Ⅰ）根据表中数据画出散点图如下所示：

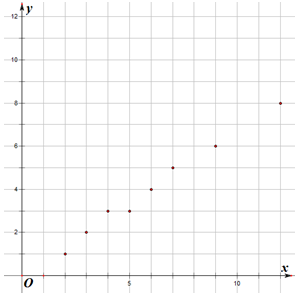
    （Ⅱ）依题意，计算$\overline x$=$\frac{1}{8}$（2+3+4+5+6+7+9+12）=6，
    $\overline y$=$\frac{1}{8}$（1+2+3+3+4+5+6+8）=4，
    $\sum_{i=1}^8{x{\;}_i^2}=4+9+16+25+36+49+81+144=364$，
    $\sum_{i=1}^8{x_i}{y_i}=2+6+12+15+24+35+54+96=244$，
    求回归系数为$\widehatb=\frac{{\sum_{i=1}^8{x_i}{y_i}-8\overline x\overline y}}{{\sum_{i=1}^8{x{\;}_i^2}-8{{\overline x}^2}}}=\frac{244-8×6×4}{{364-8×{6^2}}}=\frac{52}{76}=0.68$，
    ∴$\widehata=4-0.68×6=-0.08$；
    ∴回归直线方程为$\widehaty=0.68x-0.08$．
    （Ⅲ）由（Ⅱ）可知当x=40时，y=0.68×40-0.08≈27，
    故买进土豆40吨，预计可销售27天．

    点评 本题考查了回归直线方程的求法与应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．已知双曲线C1：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左顶点为M，抛物线C2：y2=-2ax的焦点为F，若在曲线C1的渐近线上存在点P使得PM⊥PF，则双曲线C1离心率的取值范围是（　　）
    A．（1，2）B．$（{1，\frac{{3\sqrt{2}}}{4}}]$C．（1，+∞）D．$（{\frac{{3\sqrt{2}}}{4}，2}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若x，y满足约束条件$\left\{\begin{array}{l}x-y+1≤0\\ x+y-3≥0\\ y≤4\end{array}\right.$则z=ax+y的最小值为1，则正实数a的值为（　　）
    A．10B．8C．3D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在平面直角坐标系xOy中，直线l的参数方程为 $\left\{\begin{array}{l}{x=m+\sqrt{2}t}\\{y=\sqrt{2}t}\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2=$\frac{4}{1+si{n}^{2}θ}$，且直线l经过曲线C的左焦点F．
    （ I ）求直线l的普通方程；
    （Ⅱ）设曲线C的内接矩形的周长为L，求L的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知函数$f（x）=2sin（\frac{π}{4}-2x）$，则函数f（x）的单调递减区间为（　　）
    A．$[{\frac{3π}{8}+2kπ，\frac{7π}{8}+2kπ}]（k∈Z）$B．$[{-\frac{π}{8}+2kπ，\frac{3π}{8}+2kπ}]（k∈Z）$
    C．$[{\frac{3π}{8}+kπ，\frac{7π}{8}+kπ}]（k∈Z）$D．$[{-\frac{π}{8}+kπ，\frac{3π}{8}+kπ}]（k∈Z）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知a=21.3，b=40.7，c=log38，则a，b，c的大小关系为（　　）
    A．a＜c＜bB．b＜c＜aC．c＜a＜bD．c＜b＜a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某农科所发现，一种作物的年收获量 y（单位：kg）与它“相近”作物的株数 x具有线性相关关系（所谓两株作物“相近”是指它们的直线距离不超过 1m），并分别记录了相近作物的株数为 1，2，3，5，6，7时，该作物的年收获量的相关数据如表：
    x123567
    y605553464541
    （1）求该作物的年收获量 y关于它“相近”作物的株数x的线性回归方程；
    （2）农科所在如图所示的直角梯形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，图中
    每个小正方形的边长均为 1，若从直角梯形地块的边界和内部各随机选取一株该作物，求这两株作物“相
    近”且年产量仅相差3kg的概率．
    附：对于一组数据（x1，y1），（x2，y2），…，（xn，yn），其回归直线y=bx+a的斜率和截距的最小二乘估
    计分别为，$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$a=\overline y-b\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设x，y满足约束条件$\left\{\begin{array}{l}x+y≥2\\ x-y≤2\\ y≥1\end{array}\right.$，则目标函数z=x+2y的最小值为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在（1-x3）（2+x）6的展开式中，x5的系数是-228．（用数字作答）

    查看答案和解析>>

    同步练习册答案