
 如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=14.
如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=14. 分析 解法一:当Q选在短轴的端点上,取Q(0,$\sqrt{5}$),由于A1(-3,0),A2(3,0)根据直线的斜率公式代入椭圆方程,即可求得T点坐标,则|OS|2+|OT|2=7+7=14;
解法二:设直线OS,OT的方程分别为:y=k1x,y=k2x,代入椭圆方程求得x12=$\frac{45}{5+9{k}_{1}^{2}}$,y12=$\frac{45{k}_{1}^{2}}{5+9{k}_{1}^{2}}$,x22=$\frac{45}{5+9{k}_{2}^{2}}$,y22=$\frac{45{k}_{2}^{2}}{5+9{k}_{2}^{2}}$,由k1•k2=$\frac{{y}_{0}}{{x}_{0}+3}$•$\frac{{y}_{0}}{{x}_{0}-3}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-9}$=-$\frac{5}{9}$,根据两点之间的距离公式即可求得|OS|2+|OT|2的值.
解答 解法一:题目为选择题,可采用特殊点法进行快速计算,
由椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$焦点在x轴上,
当Q选在短轴的端点上,取Q(0,$\sqrt{5}$),
由于A1(-3,0),A2(3,0)
则QA1斜率为k=$\frac{\sqrt{5}}{3}$,
即直线OT为y=$\frac{\sqrt{5}}{3}$x,
$\left\{\begin{array}{l}{y=\frac{\sqrt{5}}{3}x}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=±\frac{3}{\sqrt{2}}}\\{y=±\sqrt{\frac{5}{2}}}\end{array}\right.$,可得T点横纵坐标($\frac{3}{\sqrt{2}}$,$\sqrt{\frac{5}{2}}$)
则由对称可知OS=OT=$\sqrt{\frac{9}{2}}+\frac{5}{2}$=$\sqrt{7}$,
则|OS|2+|OT|2=7+7=14,
故答案为:14.
解法二:设Q(x0,y0),S(x1,y1),T(x2,y2),
则$\frac{{x}_{0}^{2}}{9}+\frac{{y}_{0}^{2}}{5}=1$,y02=$\frac{5}{9}$(9-x02),
设直线OS,OT的方程分别为:y=k1x,y=k2x,
则${k}_{{A}_{2}Q}$=k1,${k}_{{A}_{1}Q}$=k2.
由k1•k2=$\frac{{y}_{0}}{{x}_{0}+3}$•$\frac{{y}_{0}}{{x}_{0}-3}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-9}$=-$\frac{5}{9}$,
则$\left\{\begin{array}{l}{y={k}_{1}x}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1}\end{array}\right.$,解得:x12=$\frac{45}{5+9{k}_{1}^{2}}$,y12=$\frac{45{k}_{1}^{2}}{5+9{k}_{1}^{2}}$,
同理可知:x22=$\frac{45}{5+9{k}_{2}^{2}}$,y22=$\frac{45{k}_{2}^{2}}{5+9{k}_{2}^{2}}$,
由两点之间的距离公式可知:|OS|2+|OT|2=x12+y12+x22+y22=$\frac{45(1+{k}_{1}^{2})}{5+9{k}_{1}^{2}}$+$\frac{45(1+\frac{25}{81{k}_{1}^{2}})}{5+9×\frac{25}{81{k}_{1}^{2}}}$=$\frac{70+126{k}_{1}^{2}}{5+9{k}_{1}^{2}}$=14,
故答案为:14.
点评 本题考查直线与椭圆的位置关系,直线的斜率公式,直线与椭圆相交弦长问题、平行四边形的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{4\sqrt{3}}}{5}$ | B. | $-\frac{{3\sqrt{3}}}{5}$ | C. | $\frac{{3\sqrt{3}}}{5}$ | D. | $\frac{{4\sqrt{3}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知一个多面体的三视图如图示:其中正视图与侧视图都是边长为1的等腰直角三角形,俯视图是边长为1的正方形,若该多面体的顶点都在同一个球面上,则该球的表面积为3π.
已知一个多面体的三视图如图示:其中正视图与侧视图都是边长为1的等腰直角三角形,俯视图是边长为1的正方形,若该多面体的顶点都在同一个球面上,则该球的表面积为3π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
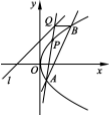 过点C(2,2)作一直线与抛物线y2=4x交于A,B两点,点P是抛物线y2=4x上到直线l:y=x+2的距离最小的点,直线AP与直线l交于点Q.
过点C(2,2)作一直线与抛物线y2=4x交于A,B两点,点P是抛物线y2=4x上到直线l:y=x+2的距离最小的点,直线AP与直线l交于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4,5,6} | B. | {1,3,5} | C. | {2,4,6} | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com