
分析 (1)求出函数的导数,问题转化为$a≥{(\frac{lnx+1}{x})_{max}}x∈(0,+∞)$,令$g(x)=\frac{lnx+1}{x}x∈(0,+∞)$,根据函数的单调性求出g(x)的最大值,从而求出a的范围即可;
(2)求出函数f(x)的导数,令F(x)=f'(x)=lnx-ax+1,求出函数F(x)的导数,通过讨论a的范围求出a的范围,证明即可.
解答 解:(1)因为f'(x)=lnx-ax+1(x>0),
所以由f'(x)≤0在(0,+∞)上恒成立得$a≥{(\frac{lnx+1}{x})_{max}}x∈(0,+∞)$,
令$g(x)=\frac{lnx+1}{x}x∈(0,+∞)$,易知g(x)在(0,1)单调递增(1,+∞)单调递减,
所以a≥g(1)=1,
即得:a≥1…(5分)
(2)函数y=f(x)有两个极值点x1,x2(x1<x2),
即y=f'(x)有两个不同的零点,且均为正,f'(x)=lnx-ax+1(x>0),
令F(x)=f'(x)=lnx-ax+1,由$F'(x)=\frac{1}{x}-a=\frac{1-ax}{x}(x>0)$可知
1)a≤0时,函数y=f(x)在(0,+∞)上是增函数,不可能有两个零点.
2)a>0时,y=F(x)在$(0,\frac{1}{a})$是增函数在$(\frac{1}{a},+∞)$是减函数,
此时$f(\frac{1}{a})$为函数的极大值,也是最大值.
当$F(\frac{1}{a})≤0$时,最多有一个零点,所以$F(\frac{1}{a})=ln\frac{1}{a}>0$才可能有两个零点,
得:0<a<1…(7分)
此时又因为$\frac{1}{e}<\frac{1}{a}<\frac{e^2}{a^2}$,$F(\frac{1}{e})=-\frac{a}{e}<0$,$F(\frac{e^2}{a^2})=3-2lna-\frac{e^2}{a}(0<a<1)$,
令$φ(a)=3-2lna-\frac{e^2}{a},φ'(a)=-\frac{2}{a}+\frac{e^2}{a^2}=\frac{{{e^2}-2a}}{a^2}>0$,φ(a)在(0,1)上单调递增,
所以φ(a)<φ(1)=3-e2,即$φ(\frac{e^2}{a^2})<0$
综上,所以a的取值范围是(0,1)…(8分)
下面证明x1+x2>2
由于y=F(x)在$(0,\frac{1}{a})$是增函数在$(\frac{1}{a},+∞)$是减函数,$0<{x_1}<\frac{1}{a}$,可构造出$\frac{2}{a}-{x_1}>\frac{1}{a}$
构造函数 $m(x)=F(\frac{2}{a}-x)-F(x)=ln(\frac{2}{a}-x)-a(\frac{2}{a}-x)-(lnx-ax)(0<x≤\frac{1}{a})$
则$m'(x)=\frac{1}{{x-\frac{2}{a}}}-\frac{1}{x}+2a=\frac{{2a{{(x-\frac{1}{a})}^2}}}{{x(x-\frac{2}{a})}}<0$,故m(x)在区间$(0,\frac{1}{a}]$上单调减.又由于$0<{x_1}<\frac{1}{a}$,
则$m({x_1})>m(\frac{1}{a})=0$,即有m(x1)>0在$(0,\frac{1}{a})$上恒成立,即有$F(\frac{2}{a}-{x_1})>F({x_1})=F({x_2})$成立.
由于${x_2}>\frac{1}{a}$,$\frac{2}{a}-{x_1}>\frac{1}{a}$,y=F(x)在$(\frac{1}{a},+∞)$是减函数,所以${x_2}>\frac{2}{a}-{x_1}$
所以${x_1}+{x_2}>\frac{2}{a}>2$成立 …(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 最小值为e-1,没有最大值 | B. | 最大值为e2-2,没有最小值 | ||
| C. | 既没有最大值,也没有最小值 | D. | 最小值为e-1,最大值为e2-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=14.
如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=14.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 1 | B. | $\sqrt{2015}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2017}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{33}{65}$或$\frac{63}{65}$ | B. | $\frac{63}{65}$ | C. | $\frac{33}{65}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
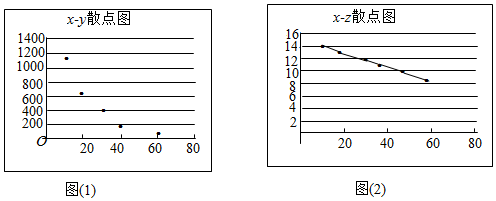
| 定价x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| z=2lny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com