
| A. | $-\frac{{4\sqrt{3}}}{5}$ | B. | $-\frac{{3\sqrt{3}}}{5}$ | C. | $\frac{{3\sqrt{3}}}{5}$ | D. | $\frac{{4\sqrt{3}}}{5}$ |
分析 利用同角三角函数的基本关系求得sin(α+$\frac{2π}{3}$)的值,再利用两角和差的三角公式求得 cosα=cos[(α+$\frac{2π}{3}$)-$\frac{2π}{3}$]以及sinα=sin[(α+$\frac{2π}{3}$)-$\frac{2π}{3}$]的值,可得要求式子的值.
解答 解:∵$cos(α+\frac{2}{3}π)=\frac{4}{5},-\frac{π}{2}<α<0$,∴sin(α+$\frac{2π}{3}$)=$\sqrt{{1-cos}^{2}(α+\frac{2π}{3})}$=$\frac{3}{5}$,
而 cosα=cos[(α+$\frac{2π}{3}$)-$\frac{2π}{3}$]=cos(α+$\frac{2π}{3}$)cos$\frac{2π}{3}$+sin(α+$\frac{2π}{3}$)sin$\frac{2π}{3}$=$\frac{3\sqrt{3}-4}{10}$,
∴sinα=sin[(α+$\frac{2π}{3}$)-$\frac{2π}{3}$]=sin(α+$\frac{2π}{3}$)cos$\frac{2π}{3}$-cos(α+$\frac{2π}{3}$)sin$\frac{2π}{3}$=$\frac{-3-4\sqrt{3}}{10}$,
则$sin(α+\frac{π}{3})+sinα$=sinαcos$\frac{π}{3}$+cosαsin$\frac{π}{3}$+sinα=$\frac{3}{2}$sinα+$\frac{\sqrt{3}}{2}$cosα=-$\frac{4\sqrt{3}}{5}$,
故选:A.
点评 本题主要考查同角三角函数的基本关系,两角和差的三角公式的应用,属于基础题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:选择题
 如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )
如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值为e-1,没有最大值 | B. | 最大值为e2-2,没有最小值 | ||
| C. | 既没有最大值,也没有最小值 | D. | 最小值为e-1,最大值为e2-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪(2,+∞) | B. | (-∞,-2)∪(1,+∞) | C. | (1,2) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=14.
如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=14.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
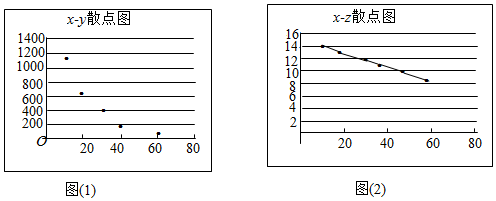
| 定价x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| z=2lny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com