
 ij��������ѧ��Ůͯ�У������ȡ50���������ߣ���λ��cm����Ƶ�ʷֲ��������
ij��������ѧ��Ůͯ�У������ȡ50���������ߣ���λ��cm����Ƶ�ʷֲ��������| ���飨���ߣ� | [80��85�� | [85��90�� | [90��95�� | [95��100�� |
| Ƶ���������� | 5 | 10 | 20 | 15 |
���� ��1������Ƶ�ʷֲ�ֱ��ͼ�Ļ�����ͼ���ɣ�
��2������������[80��85����Ƶ����ռ�ı��������������[80��85���ĸ�����
��3�����оٷ�������еĻ����¼��ĸ���������������������¼��ĸ��������ɵõ������¼��ĸ��ʣ�
��� �⣺��1��
��2�������÷ֲ�����ķ�����������[80��85����[95��100����Ůͯ�й���ȡ4������������[80��85��������=$\frac{5}{5+15}��4=1$��
��3������[80��85���г�ȡ����ŮͯΪx����[95��100���г�ȡ����Ůͯ�ֱ�Ϊa��b��c��
�ӳ����4��Ůͯ�У���ȡ2�������У�x��a������x��b������x��c������a��b������a��c������b��c��6����������з��ϡ�������[80��85����[95��100���и���һ������������У�x��a������x��b������x��c���֣�
��������[80��85����[95��100���и���1�˵ĸ���Ϊ$\frac{3}{6}=\frac{1}{2}$��
���� ���⿼��ŵ�������⣬���оٷ���������оٳ������¼��������������¼���Ӧ���оٷ�����������һ���ֵ�����Ҫ˼�룮�������ֲ�����Ķ���ͷ����������������и���ĸ�����֮�ȵ��������ж�Ӧ�����������֮�ȣ����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | 102 | 126 | 131 | 118 | 127 |
| �� | 96 | 117 | 120 | 119 | 135 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
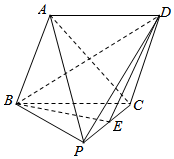 ��ͼ��������P-ABCD�У�����ABCD�����Σ�����PBC��ֱ�������Σ���PCB=90�㣬��E��PC���е㣬��ƽ��PBC��ƽ��ABCD��֤����
��ͼ��������P-ABCD�У�����ABCD�����Σ�����PBC��ֱ�������Σ���PCB=90�㣬��E��PC���е㣬��ƽ��PBC��ƽ��ABCD��֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 20 | C�� | 27 | D�� | 40 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b-1 | B�� | a��b+1 | C�� | a2��b2 | D�� | $\frac{1}{a}$��$\frac{1}{b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 5 | C�� | 8 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Vp | B�� | �Vq | C�� | ���Vp����q | D�� | p�ţ��Vq�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2��3��4��5} | B�� | {2��3��4} | C�� | {3��4��5} | D�� | {2��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com