已知函数f(x)＝ax2＋2x＋c(a，c∈N*)满足①f(1)＝5；②6<f(2)<11.
(1)求f(x)的解析式．
(2)若对任意实数x∈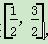
，都有f(x)－2mx≤1成立，求实数m的取值范围．
科目：高中数学 来源： 题型：
已知函数f(x)在实数集R上具有下列性质：①直线x＝1是函数f(x)的一条对称轴；②f(x＋2)＝－f(x)；③当1≤x1<x2≤3时，[f(x2)－f(x1)](x2－x1)<0，则f(2 011)，f(2 012)，f(2 013)从大到小的顺序为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知f(x)，g(x)分别是定义在R上的奇函数和偶函数，且f(x)－g(x)＝
x，则f(1)，g(0)，g(－1)之间的大小关系是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
设二次函数f(x)＝ax2－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是( )
A．(－∞，0] B．[2，＋∞)
C．(－∞，0]∪[2，＋∞) D．[0,2]
查看答案和解析>>
科目：高中数学 来源： 题型：
设集合A＝{x||x－1|<2}，B＝{y|y＝2x，x∈[0,2]}，则A∩B＝ ( )
A．[0,2] B．(1,3)
C．[1,3) D．(1,4)
查看答案和解析>>
科目：高中数学 来源： 题型：
已知某食品厂生产100克饼干的总费用为1.80元，现该食品厂对饼干采用两种包装，其包装费及售价如表所示：
| 型号 | 小包装 | 大包装 |
| 质量 | 100克 | 300克 |
| 包装费 | 0.5元 | 0.8元 |
| 售价 | 3.00元 | 8.40元 |
下列说法中：
①买小包装实惠；
②买大包装实惠；
③卖3包小包装比卖1包大包装盈利多；
④卖1包大包装比卖3包小包装盈利多．
所有正确的说法是( )
A．①④ B．①③
C．②③ D．②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
<a<
，故a＝1，c＝2.
上恒成立，易求
＝－
，
.
，则f(x)的单调递减区间是________．
上的值域．