
分析 (1)求出原函数的导函数,利用导数在各区间内的符号,可求函数f(x)单调区间;
(2)①先证明当a>1时,对任意的x>0,有f(x)>f(-x)成立,当0<a<1时,对任意的x>0,有f(x)>f(-x)成立,再分情况讨论可得.
②问题等价于f(x)在[-1,1]的最大值与最小值之差≤e-1.由(1)可知f(x)在[-1,0]上递减,在[0,1]上递增,f(x)的最小值为f(0)=1,最大值等于f(-1),f(1)中较大的一个,构造函数可得f(x)的最大值为f(1)=a+1-lna,从而问题转化为a-lna≤e-1,即可求得a的取值范围.
解答 解:(Ⅰ)函数f(x)的定义域为R,f'(x)=axlna+2x-lna=2x+(ax-1)lna.
令h(x)=f'(x)=2x+(ax-1)lna,h′(x)=2+axln2a,
当a>0,a≠1时,h'(x)>0,所以h(x)在R上是增函数,
又h(0)=f′(0)=0,所以,f'(x)>0的解集为(0,+∞),f′(x)<0的解集为(-∞,0),
故函数f(x)的单调增区间为(0,+∞),单调减区间为(-∞,0);
(2)①由(1)可知m1≠m2,当f(m1)=f(m2)时,m1,m2异号,不妨设有m1>0,m2<0,
先证明一个结论
当a>1时,对任意的x>0,有f(x)>f(-x)成立,
当0<a<1时,对任意的x>0,有f(x)>f(-x)成立,
∵f(x)>f(-x)
∴ax+x2-xlna>a-x+xx+xlna?ax+a-x-2xlna,
令t(x)=ax+a-x-2xlna,
∵t′(x)=axlna+a-xlna-2lna=lna(ax+a-x-2)≥2$\sqrt{{a}^{x}•{a}^{-x}}-2$=0,(当且仅当x=0时等号成立),
又t(0)=0,
当a∈(0.,1)时,t′(x)≤0,所以t (x)在(0,-∞)上单调递减,
t(x)<t(0)=0,
此时对任意的x>0,有f(x)<f(-x)成立,
当a∈(1,+∞),t′(x)>0,所以t (x)在(1,+∞)上单调递增,
此时对任意的x>0,有f(x)>f(-x)成立.
当a>1时,f(m2)=f(m1)>f(-m1),由于f(x)在(-∞,0)上单调递减,所以m2<-m1,m1+m2<0.
同理0<a<1,m1+m2>0.
当f(m1)=f(m2)时,当且仅当a>1时,有m1+m2<0成立.
②:问题等价于f(x)在[-1,1]的最大值与最小值之差≤e-1.
由(1)可知f(x)在[-1,0]上递减,在[0,1]上递增,
∴f(x)的最小值为f(0)=1,最大值等于f(-1),f(1)中较大的一个,
f(-1)=$\frac{1}{a}$+1lna,f(1)=a+1-lna,
f(1)-f(-1)=a-$\frac{1}{a}$-2lna,
令g(x)=x-$\frac{1}{x}$-2lnx,(x≥1),
则g′(x)=1+$\frac{1}{{x}^{2}}-\frac{2}{x}$=$(\frac{1}{x}-1)^{2}$≥0,仅在x=1时取等号,
∴g(x)为增函数,
∴当a>1时,g(a)=a-$\frac{1}{a}$-2lna>g(1)=0,
即f(1)-f(-1)>0,∴f(1)>f(-1),
于是f(x)的最大值为f(1)=a+1-lna,
故对?x1,x2∈[-1,1],|f(x1)-f(x2)|≤|f(1)-f(0)|=a-lna,∴a-lna≤e-1,
当x≥1时,(x-lnx)′=$\frac{x-1}{x}$≥0,
∴y=x-lnx在[1,+∞)单调递增,
∴由a-lna≤e-1可得a的取值范围是1<a≤e.
当0<a<1,此时,f(-1)为最大值,即f(-1)=$\frac{1}{a}$+1+lna,
∴$\frac{1}{a}$+1+lna-e+1≤0,
设F′(a)=-$\frac{1}{{a}^{2}}$+$\frac{1}{a}$=$\frac{a-1}{{a}^{2}}$<0,
∴F(a)在(0,1)单调递减,
∵F($\frac{1}{e}$)=e-1-e+1=0,由F′(a)≤0,解得$\frac{1}{e}$≤a<1,
综上所述a的取值范围为[$\frac{1}{e}$,1)∪(1,e].
点评 本题考查利用导数研究函数的单调性,考查恒成立问题的求解方法,考查学生分析问题和解决问题的能力,解题的关键是利用导数确定函数的最值,属难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
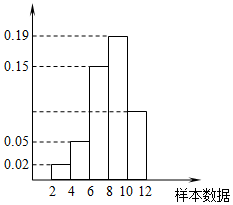 有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
有一个容量为300的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )| A. | 27 | B. | 81 | C. | 54 | D. | 108 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车站在春运期间为了改进服务,随机抽样调查了若干名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位为min),下表和下图是这次调查统计分析所得到的频率分布表和频率分布直方图,解答下列问题:
某车站在春运期间为了改进服务,随机抽样调查了若干名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位为min),下表和下图是这次调查统计分析所得到的频率分布表和频率分布直方图,解答下列问题:| 组别 | 分组 | 频数 | 频率 |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | y |
| 四组 | 15≤t<20 | x | 0.50 |
| 五组 | 20≤t<25 | 30 | 0.30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com