
分析 (1)先分别求出集合B,C,再根据A∩B=A∪B,得到A=B,根据根与系数的关系即可求出a的值;
(2)由A∩B=A∩C≠∅,得到A∩B=A∩C={2},即2∈A,代入解得a的值,并需要验证.
解答 解:(1)B={x|x2-5x+6=0},C={x|2x2-5x+2=0},
∴B={2,3},C={2,$\frac{1}{2}$},
∵A∩B=A∪B,
∴A=B,
∵A={x|x2+(4-a2)x+a+3=0},
∴4-a2=-(2+3),a+3=2×3,解得a=3,
(2)∵A∩B=A∩C≠∅,
∴A∩B=A∩C={2},
∴2∈A,
∴22+2(4-a2)+a+3=0 即2a2-a-15=0
解得a=3或a=-$\frac{5}{2}$,
当a=3时,A={2,3} 此时A∩B≠A∩C 舍去;
当a=-$\frac{5}{2}$时,A={2,$\frac{1}{4}$} 此时满足题意.
综上,a=-$\frac{5}{2}$.
点评 本题题主要考查子集的定义及其有方程的解法,集合的交集及并集集运算,属于基础题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:解答题
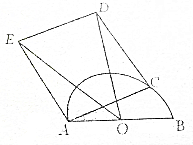 如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.
如图,线段AB长度为2,以AB为直径作半圆O,又以半圆O的一条弦AC为边作正方形ACDE,设△OED的面积为S,∠CAB=α.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 14 | C. | 18 | D. | $14\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com