
分析 (1)由条件①②③得出f(x)的最小正周期和最小值,从而求出ω、φ和A的值,即得f(x)的解析式;
(2)根据题意,利用三角恒等变换,即可求出sin($\frac{π}{6}$-2x)的值;
(3)利用换元法,把不等式化为2m+1≤t2+t有解,求出t2+t的最大值即可得出m的取值范围.
解答 解:(1)由条件①②③可知,$x=-\frac{π}{4}$和$x=\frac{π}{4}$为相邻对称轴,
且f(x)在$x=-\frac{π}{4}$处取得最大值,在$x=\frac{π}{4}$处取得最小值,
所以$\frac{T}{2}=\frac{π}{2}$,解得ω=2;
由f(x)在$x=-\frac{π}{4}$处取得最大值得φ=0,且A<0;
经过点$M(\frac{π}{6},-\sqrt{3})$,所以$Asin(2×\frac{π}{6})=-\sqrt{3}$,解得A=-2;
所以f(x)=-2sin(2x);--------(6分) (A,ω,φ各2分)
(2)因为$f(x+\frac{π}{6})=-2sin(2x+\frac{π}{3})=\frac{6}{5}$,
所以$sin(2x+\frac{π}{3})=-\frac{3}{5}$;
$sin(\frac{π}{6}-2x)=sin(\frac{π}{2}-(2x+\frac{π}{3}))=cos(2x+\frac{π}{3})=±\sqrt{1-{{sin}^2}(2x+\frac{π}{3})}=±\frac{4}{5}$;--------(9分)
(3)2m+1≤t2+t(其中t=-2sin2x∈[-2,2]),
t2+t=${(t+\frac{1}{2})^2}-\frac{1}{4}$$∈[-\frac{1}{4},6]$,
所以2m+1≤6,解得:$m≤\frac{5}{2}$.--------(12分)
点评 本题考查了三角函数f(x)=Asin(ωx+φ)的图象与性质的应用问题,也考查了转化思想与函数与不等式的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 大于10.828 | B. | 小于7.829 | C. | 小于6.635 | D. | 大于2.706 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
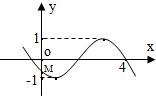 已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.
已知函数f(x)=Asin(ωx+φ)(x∈R),且A>0,ω>0,-π≤φ≤0.若f(x)的部分图象如图,且与y轴交点M(0,-$\frac{{\sqrt{2}}}{2}$),则ω+φ=-$\frac{5π}{16}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 组距 | (1,2] | (2,3] | (3,4] | (4,5] | (5,6] | (6,7] |
| 频数 | 1 | 1 | 2 | 3 | 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com