Question

1．在直角三角形ABC中，直角顶点为C，其中∠B=60°，在角ACB内部任作一条射线CM，与线段AB交于点M，满足AM＜AC的概率为$\frac{5}{6}$，则满足BC＜AM＜AC的概率为（　　）

• A． $\frac{1}{4}$
• B． $\frac{1}{3}$
• C． $\frac{1}{2}$
• D． $\frac{2}{3}$

Answer 1

分析 由于过直角顶点C在∠ACB内部任作一射线CM，故可以认为所有可能结果的区域为∠ACB，可将事件A构成的区域为∠ACC'，以角度为“测度”来计算

解答 解：在AB上取AC'=AC，则∠ACC′=75°．
记A={在∠ACB内部任作一射线CM，与线段AB交于点M，AM＜AC}，
则所有可能结果的区域为∠ACB，
事件A构成的区域为∠ACC'．
又∠ACB=90°，∠ACC'=75°．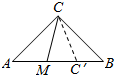
又满足BC＜AM的事件为B，则事件B是∠ACC'=60°的区域，所以满足BC＜AM＜AC的角度区域为事件A，B的同时发生，即∠MCC'=45°，
由几何概型公式得到BC＜AM＜AC的概率为：$\frac{45°}{90°}=\frac{1}{2}$；
故选：C．

点评 本题考查几何概型．在利用几何概型的概率公式来求其概率时，几何“测度”可以是长度、面积、体积、角度等，其中对于几何度量为长度，面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的．