练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．化简：$\frac{sin（-α+180°）-tan（-α）+tan（-α+360°）}{tan（α+180°）+cos（-α）+cos（α+180°）}$．

    分析 原式利用诱导公式化简，再利用同角三角函数间基本关系变形，约分即可得到结果．

    解答 解：原式=$\frac{sinα+tanα-tanα}{tanα+cosα-cosα}$=$\frac{sinα}{\frac{sinα}{cosα}}$=cosα．

    点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．已知平行四边形ABCD的三个顶点A，B，C分别对应复数3+3i，-2+i，-5i，则第四个顶点D对应的复数为5-3i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．某几何体三视图如图（单位；cm），则该几何体的体积是（　　）
    A．1500cm3B．1025cm3C．625cm3D．1200cm3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某校进行新课程改革已经四年，为了解教师对新课程改革教学模式的使用情况，进行问卷调查，共调查了50人，其中老教师20人，青年教师30人，老教师对新课改革赞同的有10人，不赞同的10人，青年教师中赞中的24人．
    （1）根据以上数据建立一个2×2列联表；
    （2）判断是否有99%的把握说明对新课程模式的赞同情况与年龄有关？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

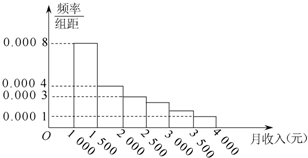    19．如图是某市有关部门根据该市干部的月收入情况，作抽样调查后画出的样本频率分布直方图．已知图中第一组的频数为4000，请根据该图提供的信息 （图中每组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）），回答：
    （1）若按月收入用分层抽样方法抽出100人，则月收入在[1500，2000）的这段应抽20人
    （2）样本数据的中位数估计为1750（元）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知A（2，-1）、B（3，2）、C（-3，-1），BC边上的高为AD，求向量$\overrightarrow{AD}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．函数y=3sinx-4cosx，x∈[0，π]的值域为[-4，5]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=x2-ax+a-1，a∈R．
    （1）若f（x）在区间[0，2]上单调，求a的取值范围；
    （2）若对于任意a∈（0，4），存在x0∈[0，2]，使得t≤|f（x0）|成立，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列选项中，说法正确的是（　　）
    A．若命题“p∨q”为真命题，则命题p和命题q均为真命题
    B．am2＜bm2是a＜b的必要不充分条件
    C．x=2kπ+$\frac{π}{4}$（k∈Z）是（-sinx）′=（cosx）′的充要条件
    D．命题“若{$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{b}$+$\overrightarrow{c}$，$\overrightarrow{c}$+$\overrightarrow{a}$}构成空间的一个基底，则{$\overrightarrow{a}$，$\overrightarrow{b}$$\overrightarrow{c}$}构成空间的一个基底”的否命题为真命题

    查看答案和解析>>

    同步练习册答案