
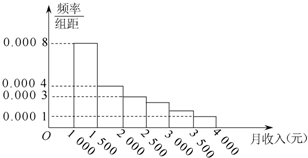
 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:分析 (1)先求出月收入在[1500,2000)内的频率,再利用分层抽样原理求出应抽的人数;
(2)根据中位数的两边频率相等,求出这组数据的中位数.
解答 解:(1)根据频率分布直方图,得:
月收入在[1500,2000)内的频率为:0.0004×(2000-1500)=0.2,
∴用分层抽样法在这段应抽:100×0.2=20人;
(2)∵0.0008×500=0.4<0.5,
0.4+0.2=0.6>0.6,
∴中位数应在[1500,2000)内,可设为x,
则0.4+(x-1500)×0.0004=0.5,
解得x=1750,
即中位数是1750.
故答案为:20,1750.
点评 本题考查了频率分布直方图的应用问题,也考查了分层抽样方法的应用问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个空间几何体的三视图,该几何体的外接球的体积为( )
如图是一个空间几何体的三视图,该几何体的外接球的体积为( )| A. | 8$\sqrt{2}$ | B. | $\frac{8\sqrt{2}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{16\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com