
分析 (1)由已知得到向量$\overrightarrow{AD}$,利用向量平行求n;
(2)求出$\overrightarrow{AC}$,$\overrightarrow{BD}$的坐标,由向量垂直,数量积为0 求m.
解答 解:因为$\overrightarrow{AB}$=(-1,3),$\overrightarrow{BC}$=(3,m),$\overrightarrow{CD}$=(1,n),所以$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}$=(3,3+m+n),
(1)因为$\overrightarrow{AD}$∥$\overrightarrow{BC}$.所以$\overrightarrow{AD}=λ\overrightarrow{BC}$,即$\left\{\begin{array}{l}{3=3λ}\\{3+m+n=λm}\end{array}\right.$,解得n=-3;
(2)因为$\overrightarrow{AC}$=$\overrightarrow{AB}+\overrightarrow{BC}$=(2,3+m),$\overrightarrow{BD}$=$\overrightarrow{BC}+\overrightarrow{CD}$=(4,m-3),又$\overrightarrow{AC}$⊥$\overrightarrow{BD}$,
所以$\overrightarrow{AC}$•$\overrightarrow{BD}$=0,
即8+(3+m)(m-3)=0,解得m=±1.
点评 本题考查了向量平行和垂直的性质运用;关键是明确坐标关系.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
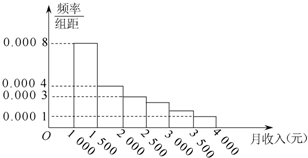 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com