
分析 (1)由已知椭圆的离心率得到a,b的关系,结合双曲线的焦点坐标求得椭圆的短半轴,结合隐含条件得答案;
(2)①设出直线方程,联立直线方程和椭圆方程,由判别式大于0求得k的范围,把$\overrightarrow{OA}•\overrightarrow{OB}$代入根与系数关系化为含有k的代数式,由k的范围求得$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围;
②求出B点关于x轴的对称点的坐标,写出直线AG的方程,求得与x轴的交点的横坐标,代入①的根与系数关系得答案.
解答 (1)解:由题意知,$\frac{c}{a}$=$\frac{1}{2}$,b=$\sqrt{3}$
∴c=1,a=2.
∴故椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)①解:由题意知直线l的斜率存在,设直线l的方程为y=k(x-4),
代入椭圆方程,整理得(3+4k2)x2-32k2x+64k2-12=0.
由△=(-32k2)2-4•(3+4k2)(64k2-12)>0,得:-$\frac{1}{2}$<k<$\frac{1}{2}$.
设A(x1,y1),B (x2,y2),
则x1+x2=$\frac{32{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{64{k}^{2}-12}{3+4{k}^{2}}$①,
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(1+k2)x1x2-4k2(x1+x2)+16k2=25-$\frac{87}{4{k}^{2}+3}$,
∴$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围是[-4,$\frac{13}{4}$);
②证明:∵B,G关于x轴对称,
∴点G的坐标为(x2,-y2),
直线AG的方程为y-y1=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1),
令y=0,得x=$\frac{{x}_{1}{y}_{2}+{x}_{2}{y}_{1}}{{y}_{1}+{y}_{2}}$,
又y1=k(x1-4),y2=k(x2-4),
∴x=$\frac{{x}_{1}{y}_{2}+{x}_{2}{y}_{1}}{{y}_{1}+{y}_{2}}$=$\frac{2{x}_{1}{x}_{2}-4({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}-8}$.
把①式代入得x=1.
∴直线与x轴相交于定点(1,0).
点评 本题主要考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是压轴题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
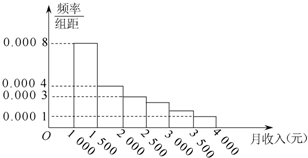 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com