
分析 (Ⅰ)由特殊角的三角函数值即可得解.
(Ⅱ) 由三角函数中的恒等变换应用化简已知等式可得16sin2α-4sinα-11=0,结合范围α∈(0,π),即可求得sinα的值.
解答 (本题10分)
解:(Ⅰ)∵$sin\frac{π}{6}=\frac{1}{2},cos\frac{π}{6}=\frac{\sqrt{3}}{2}$,
∴f($\frac{π}{6}$)=sin$\frac{π}{6}$cos$\frac{π}{6}$-$\sqrt{3}$sin2$\frac{π}{6}$=0. …(3分)
(Ⅱ) f(x)=$\frac{\sqrt{3}}{2}$cos2x-$\frac{\sqrt{3}}{2}$+$\frac{1}{2}sin2x$,…(5分)
∴f($\frac{α}{2}$)=$\frac{\sqrt{3}}{2}$cosα-$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$sinα=$\frac{1}{4}-\frac{\sqrt{3}}{2}$,整理可得:2$\sqrt{3}$cosα+2sinα=1,即:2$\sqrt{3}$$\sqrt{1-si{n}^{2}α}$=1-2sinα,
∴两边平方可得:16sin2α-4sinα-11=0,解得sinα=$\frac{1±3\sqrt{5}}{8}$,…(8分)
∵α∈(0,π),∴sinα>0,故sinα=$\frac{1+3\sqrt{5}}{8}$.….(10分)
点评 本题主要考查了三角函数中的恒等变换应用,属于基本知识的考查.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:选择题
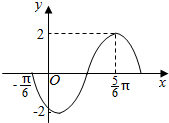 已知函数f(x)=2sin(ωx+φ),(ω>0,0<φ<2π)的部分图象如图所示,则f(x)的表达式为( )
已知函数f(x)=2sin(ωx+φ),(ω>0,0<φ<2π)的部分图象如图所示,则f(x)的表达式为( )| A. | $f(x)=2sin(\frac{4}{3}x+\frac{2}{9}π)$ | B. | $f(x)=2sin(\frac{4}{3}x+\frac{25}{18}π)$ | ||
| C. | $f(x)=2sin(\frac{3}{2}x+\frac{π}{4})$ | D. | $f(x)=2sin(\frac{3}{2}x+\frac{5}{4}π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
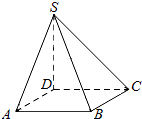 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2.
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com