考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由双曲线方程知a=2,b=3,c=
,设|MF
1|=r
1,|MF
2|=r
2(r
1>r
2).由双曲线定义,有r
1-r
2=2a=4,由此能求出△F
1MF
2的面积.
(2)若∠F
1MF
2=60°,在△MF
1F
2中,由余弦定理及双曲线定义求得r
1r
2=36.由此求出
S△F1MF2=9
.同理可求得若∠F
1MF
2=120°,
S△F1MF2=3
.
(3)由以上结果猜想,随着∠F
1MF
2的增大,△F
1MF
2的面积将减小.由双曲线定义及余弦定理能证明当θ增大时,
S△F1MF2=
将减小.
解答:
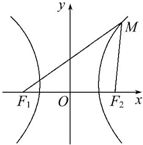
解:(1)由双曲线方程
-
=1,知a=2,b=3,c=
,
设|MF
1|=r
1,|MF
2|=r
2(r
1>r
2).
由双曲线定义,有r
1-r
2=2a=4,
两边平方得
r12+r22-2r
1•r
2=16,
∴|F
1F
2|
2-4
S△F1MF2=16,
∴52-16=4
S△F1MF2,解得
S△F1MF2=9.
∴△F
1MF
2的面积是9.(4分)
(2)若∠F
1MF
2=60°,在△MF
1F
2中,
由余弦定理得|F
1F
2|
2=
r12+r22-2r
1r
2cos 60°,
|F
1F
2|
2=(r
1-r
2)
2+r
1r
2,所以r
1r
2=36.
∴
S△F1MF2=
r
1r
2sin60°=9
.
同理可求得若∠F
1MF
2=120°,
S△F1MF2=3
..(8分)
(3)由以上结果猜想,随着∠F
1MF
2的增大,△F
1MF
2的面积将减小.
证明如下:
令∠F
1MF
2=θ,则
S△F1MF2=
r
1r
2sinθ.
由双曲线定义及余弦定理,
有
| | (r1-r2)2=4a2① | | r12+r22-2r1•r2cosθ=4c2② |
| |
②-①得r
1•r
2=
,
∴
S△F1MF2==
,
∵0<θ<π,0<
<
,
在(0,
)内,tan
是增函数.
因此当θ增大时,
S△F1MF2=
将减小.(12分)
点评:本题考查三角形面积的求法,考查随着角的变化三角形面积变化的判断与证明,解题时要认真审题,注意余弦定理的合理运用.

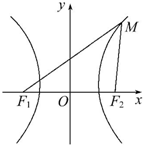 如图,设有双曲线
如图,设有双曲线 解:(1)由双曲线方程
解:(1)由双曲线方程

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案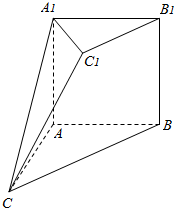 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是边长为a的正方形,AB=AC,BC=