Question

4．给出下列四个结论：
①若a、b∈[0，1]，则不等式a²+b²≤1成立的概率为$\frac{π}{4}$；
②由曲线y=x³与y=$\root{3}{x}$所围成的封闭图形的面积为0.5；
③已知随机变量ξ服从正态分布N（3，σ²），若P（ξ≤5）=m，则P（ξ≤1）=1-m；
④（$\sqrt{x}$+$\frac{1}{2\sqrt{x}}$）⁸的展开式中常数项为$\frac{35}{8}$．
其中正确结论的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 ①利用几何概型进行判断；
②作出函数图象，求出交点坐标，利用积分的几何意义，求面积即可；
③已知随机变量ξ服从正态分布N（3，σ²），则图象关于x=3对称，利用P（ξ≤1）=P（ξ≥5），可得结论；
④（$\sqrt{x}$+$\frac{1}{2\sqrt{x}}$）⁸的展开式的通项为T_r+1=${C}_{8}^{r}•{2}^{-r}•{x}^{4-r}$，令4-r=0，则r=4，可得常数项．

解答 解：①若a，b∈[0，1]，则a，b对应的平面区域为正方形，面积为1，不等式a²+b²≤1成立，对应的区域为半径为1的圆在第一象限的部分，所以面积为$\frac{π}{4}$，所以由几何概型可知不等式a²+b²≤1成立的概率是$\frac{π}{4}$．所以①正确．
②作出两个函数的图象如图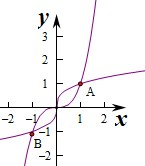：A（1，1），B（-1，-1），
由函数的对称性和积分的几何意义可知所围成的封闭图形的面积为：2${∫}_{0}^{1}$（$\root{3}{x}$-x³）dx=2（$\frac{3}{4}{x}^{\frac{4}{3}}-\frac{1}{4}{x}^{4}$）${|}_{0}^{1}$=1，故不正确；
③已知随机变量ξ服从正态分布N（3，σ²），则图象关于x=3对称，又P（ξ≤5）=m，则P（ξ≤1）=P（ξ≥5）=1-m，故正确；
④（$\sqrt{x}$+$\frac{1}{2\sqrt{x}}$）⁸的展开式的通项为T_r+1=${C}_{8}^{r}•{2}^{-r}•{x}^{4-r}$，令4-r=0，则r=4，可得常数项为$\frac{35}{8}$，故正确．
故选：C．

点评 本题主要考查了各种命题的真假判断，考查学生分析解决问题的能力，综合性较强．